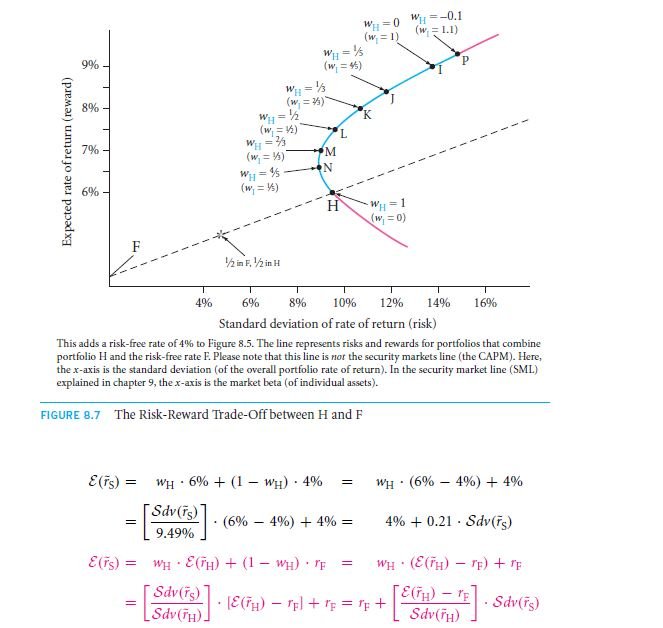
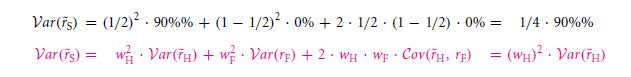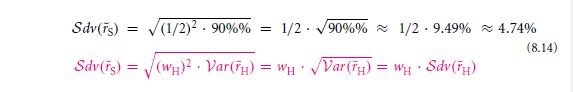For the practical world, generally we seek admittance to a Treasury that is devoid of risk totally. It happens to be the existence of an asset that is devoid of risk, and also plays a vital role, in the prototypical explanation of the subsequent lessons and in all these graphs that depict mean-variance as well. Hence, let us introduce another rate that is devoid of risks which we now call as F in to the scene. Let it be 4%. We shall commence with the three basic portfolios that are given in the following
This is done to make sure of the determining factor of the reward that you get out of this formulation. If the rate of return is to be determined, then the value can be expected to give a variance such as,
This formula proves to be much easier than the comparative ones.
As stated, the risks that are involved are not much and can be easily undone and accounted for the formula values.
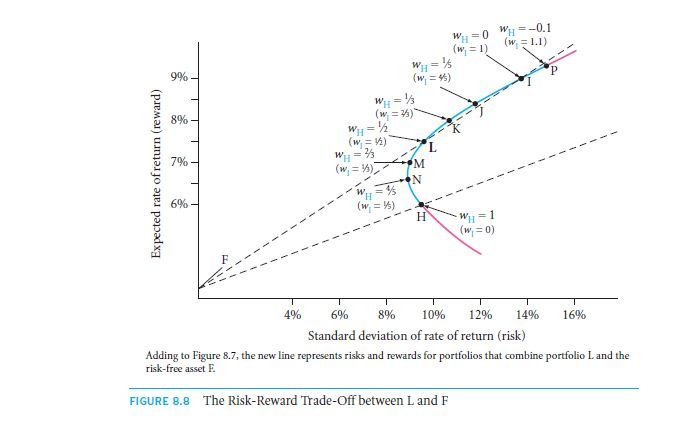
You are taught to never rely on random things and in the figure 8.8, you get an even more closer lesson on that.
CAPM Preview
Later in chapter 9 we will discuss the validation of the formulas that you act on with the solutions
In any given case, the CAPM formula will hold a steady grip on the module form.
Key terms
Solve now! Solutions
Problems
Links of Previous Main Topic:-
- Introduction of corporate finance
- The time value of money and net present value
- Stock and bond valuation annuities and perpetuities
- A first encounter with capital budgeting rules
- Working with time varying rates of return
- Uncertainty default and risk
- Risk and return risk aversion in a perfect market
- Investor choice risk and reward
Links of Next Financial Accounting Topics:-
- The capital asset pricing model
- Market imperfections
- Perfect and efficient markets and classical and behavioral finance
- Capital budgeting applications and pitfalls
- From financial statements to economic cash flows
- Valuation comparables financial ratios
- Corporate claims
- Capital structure and capital budgeting in a perfect market
- The weighted cost of capital and adjusted present value in an imperfect market with taxes
- What matters
- Equity payouts
- For value financial structure and corporate strategy analysis
- Capital structure dynamics firm scale
- Capital structure patterns in the united states
- Investment banking and mergers and acquisitions
- Corporate governance
- International finance
- Options and risk management