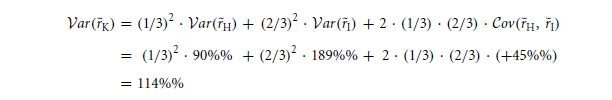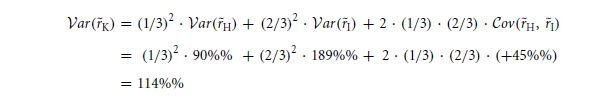There exists an easier way to make variance of portfolio calculations quicker. This easy route permits us to calculate variance of a portfolio by way of a function weights, being its parameter. For this purpose we take into account the weight of each component. To make use of it, we need to be aware of the covariance amongst all resources. The formula correspondingly skips the step of having to calculate the degree of yield first, prior to the chosen portfolio combination. This is the case with every scenario and is hardly of any issue when we have to deal with four scenarios. However the case will worsen if one has to deal with thousand observations on a daily basis. Also, that these need to be taken into account for varied scenarios and for varied port folios having different weights.
For our both the monies, you require just an extra quantity for the innovative variance easy to compute formula: You got to do calculations of the covariance between the two base ranges of investments. In our example one of them is H, while the other is I. You are by this time familiar with covariance depicted in section named 8.3B. Now, it is by definition termed as the mean product of two of the net-of-mean revenues. From the realization of each of the scenario, the mean need to be deducted (it is 6% when we consider H, while 9% as we consider I)
For two ventures, we need just an extra number for the latest variance easy formula. We have to calculate the covariance amongst the two base portfolios, we considered H and I. In section 8.3B already shows the covariance of H and I. it is the mean product of the mean product of the two net-of-mean returns. Post subtracting 6% from H and 9% from I, we get to see the following from each section:
Thus, we have
From above we can conclude that H also I are correlated in by a positive magnitude. These funds have tendency to go together. Instinctively, this implies that for instance if the rate of return or outcome on portfolio H goes above 6% of the mean, the portfolio I picks up a tendency to increase 9% of its own mean. Before further discussion let’s now see the short cut formula itself.
This summation gives off the same random valuation and guides all investors.
Following the variances we can get a correct way to address such formulas.
Yes this is it. The way to cover up the values.
All the variations are possible if and only if there are other factors that are involved like,
Links of Previous Main Topic:-
- Investor choice risk and reward
- Portfolios diversification and investor preferences
- How to measure risk contribution
- Expected rates of return and market betas for weighted portfolios and firms
- Spreadsheet calculations for risk and reward
- An investors specific trade off between risk and reward
Links of Next Financial Accounting Topics:-
- Graphing the mean variance efficient frontier
- Adding a risk free asset
- Equity payouts
- For value financial structure and corporate strategy analysis
- Capital structure dynamics firm scale
- Capital structure patterns in the united states
- Investment banking and mergers and acquisitions
- Corporate governance
- International finance
- Options and risk management