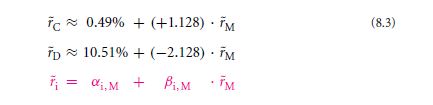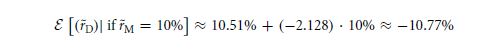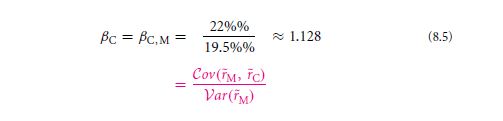With the presumption that all of our we can thrust forward that all our financiers are wise enough to have all the assets in their kitty, we must thrust forward with the quest that what are those assignments which would impart them with a good scope of extensive expansion.
8.3 A AN ASSET’S OWN RISK IS NOT A GOOD MEASURE FOR ITS RISK CONTRIBUTION TO A PORTFOLIO
Evidently extensive expansion is not of much use if two of the given prospects transfer the respect influence all the time in a particular direction. For instance say, if one seeks to expand an investment of worth $50 in A along with another venture again in A, of worth $50. These two intuitively have the equivalent results. In such a scenario, the risk would not reduce. But in another case, say if two funding chances have moved in diverse ways, then the extensive expansion venture. It works as a pair one shall feed for the gap of other.
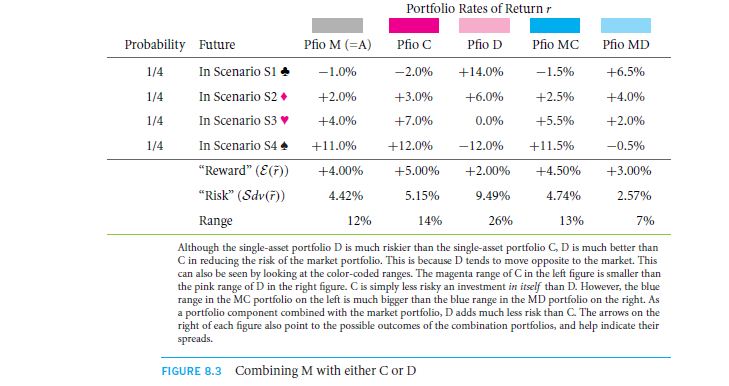
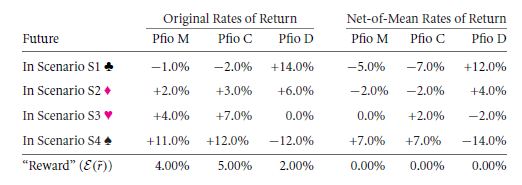
To delve more onto the depth of the case, we will go for a formal definition. With reference to the details in Table 831, we shall give the pseudonym M to the addition of stock market portfolio that is owned by financier A. Say C as well as D are the two missions on which the firm could venture, but we are in state to choose none. Return rate of C is 5% and that of D is 2%. The risk against the return for C is 5.15% and that for D is 9.49%. So, as is clear C happens to show a better scope than D. In case if you are in the managerial post, and you are supposed to decide for the stockholders, will you go for C instantly over D? Ideally, it is a No.
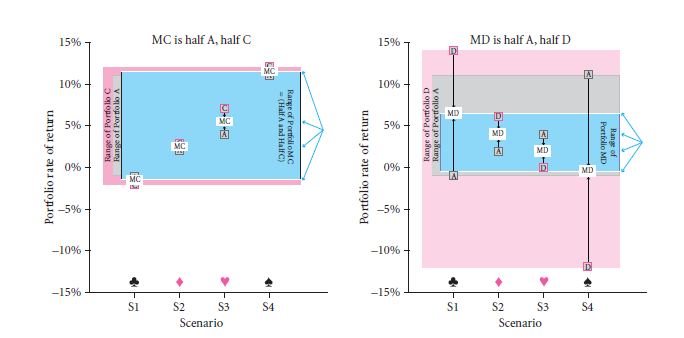
Say your funder begins with the portfolio. Now, have a look at the graphs 8.3 given below. It depicts the outcome if all the investors sell off half of the portfolio they had put on any of C alternatively D. For the purpose of explanation we can name these dual 50-50 range of investments as MC , MD correspondingly. We shall commence with MC. Say if the funders re assign half their monetary resource beginning from M ending into C, the following change is seen in the degree of return:
The graph on the left in figure 8.3 has the MC returns or outcomes, along with the return rates for M and C by itself. The area marked in magenta shows the vicinity of portfolio C, while the area that is marked grey shows the scope of portfolio A, which is M. The area that is marked blue gives a range of combination portfolio. In moving from a pure M portfolio to the MC portfolio, there involves hardly any risk, i.e. we the risk level rises from 4.42% to just 4.74%.
Now, let’s consider the MD pair. This case is shown on the graph in the right side. The area marked pink is the part to focus. It shows that on its own D is a very risky investment to make.
But if the investors instead shuffle and allocate again half of their wealth from M into D, the gross portfolio would be surely different.
There is a choice always in choosing the equity value and making the market look very attractive and appealing.
To add to the standardised value of the sum, there can be a variance that you need to simply have. Even if the qualities challenge the primal value decision of a manager.
This is done even if it means that you need to trade with a great amount of risk.
8.3 B BETA IS A GOOD MEASURE FOR AN ASSET’S RISK CONTRIBUTION TO A PORTFOLIO
So what exactly is the portfolio doing making the other ones look more attractive and appealing? It is putting forward the lifeless attorney that determines the risk factors at a test.
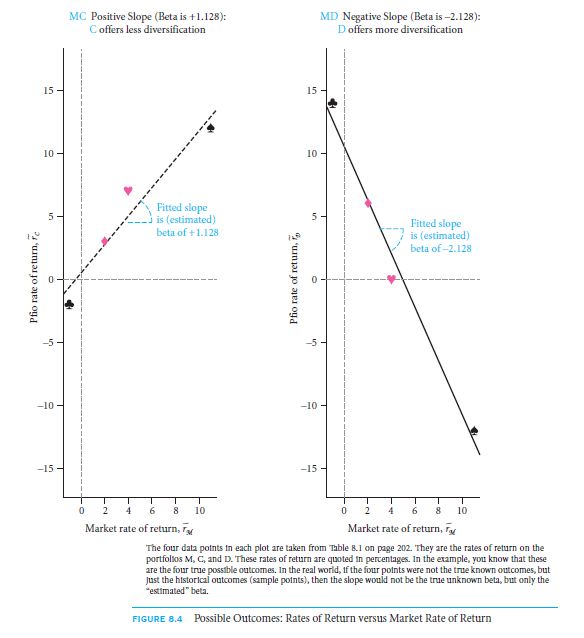
There must be a reason as to why the slope curve seems so entirely appealing. It seems like there is a need for the appropriate amount of venture. The proper risk that is incurred and the figure that 8.4 represents this deal every time.
Common measurement that is of the expectant matter, and makes a counterpart movement, is represented by the slope module. The diagram represents this by the higher slope. It appears to be a negative and hence it means that there is a better diversification in the graph.
This slope is determined by the line that is referred to as the beta value. Hence the entire formula can be written down as,
There can be beta values that are substantial. The finance is demented as that of holding and representing the market beta value. It forms up as the linear regressive method. This is so that the market gives a proper upward slope curve too.
With a subscript that finalises the proper value in the terms that include the determining factor, it is a summed up as β C, M≈ 1.128 & β D, M ≈ −2.128. This is hence called as the market model in the formula of 8.3.
There is to be minute addition the factors that are in charge. All investor get a gullible potation of the model that is to be represented. This is hence the reason why there is a great maundering law that works greatly for the investors. There is an alpha and beta value that works in a wondrous way. The market beta value gives a lawful and easy explanation.
Computing Market Betas from Historical Rates of Return
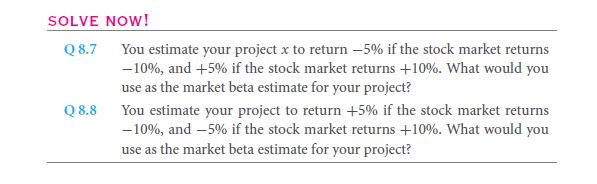
So, now that you understand the deal of the ‘beta’, how do you plan to compute that? Here in the table 8.1, I will show you on how to compute it.
First make a table,
Then place the values,
Then compute the net mean variables,
The entire statistical rate remains to be called as covariance.
There is a beta value that makes the market variance is mostly abbreviated and ratio is determined,
The correct term that is used is linear regression. This is in fact the routine that is included in the calculation that you just witnessed on the figure 8.4.
In the real world you will be able to make out the computations that are subjected into the values.
8.3C WHY NOT CORRELATION OR COVARIANCE?
There is a close inter relationship among the variances like covariance, beta along with the correlation, which is equally divided. What you must always remember is that the denominators must remain as a positive factor. Hence, there is a need to get the positive variation started.
As for the correlation that makes and gives the most perfect results, all that there is needed is a mixture of the factors. Interpretations are pretty easy if you wish to get involved with them.
Hence, as you can see, the correlations are pretty easy and basic to the factors that were already loaded and made a part of the equations.
8.3D INTERPRETING TYPICAL STOCK MARKET BETAS
The beta value that you land up as the market one, can actually hold the investor body into the beautification number. Assuming that the assumption that you took a leap at helps you to fetch investors, can help you get hold of a good trustable project.
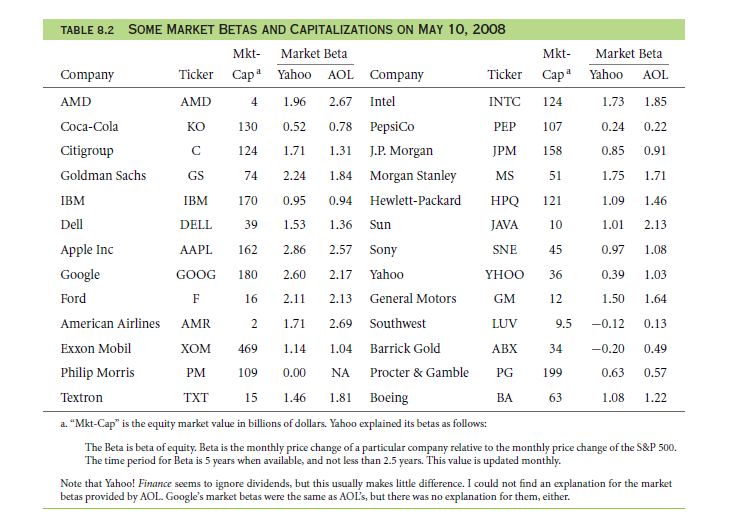
The market data value of beta can be easily looked up if you wish to, as there is a great number of certified releases made by the company. There is a back up that you can always jump back at. If you take a look at the present value, then there is a great chance at getting closer to the beta value that you targeted at.
Links of Previous Main Topic:-
Links of Next Financial Accounting Topics:-
- Expected rates of return and market betas for weighted portfolios and firms
- Spreadsheet calculations for risk and reward
- An investors specific trade off between risk and reward
- A shortcut formula for the risk of a portfolio
- Graphing the mean variance efficient frontier
- Adding a risk free asset