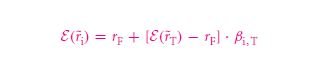There is only a small relative approach that is depicted in this book. The appendix will bring out the real deal about the area of formula that goes on.
9.7 A Math: Portfolio Separation
Mean variance efficient formulas bring in the structure that is defined. It may seem like a very silly and simplified calculation, however, it is definitely not so.
It is important to derive the formulas and hence, work along with the CAPM value that you get. The entire deal depends on the investing crowd. With a great knowledge for the risk less assets, even you can compose similar explanation.
The reverse value does not stay intact and hence needs to be taken care of. The total MVE value gets a governing hold on the assets, by making them risks free at all time. This may not be at all easy to make a definite pin point on. Though the circumstances make a willful application of the certain, there will always be a persisting sense in that.
There will not be any such behavioral conduct that gives potent advises to the investors and this is the best value evaluation that is given for the stock market value. There is a goof repercussion that is felt in the medium of the tangent line.
9.7 B Math: The Mean-Variance Efficient Frontier And CAPM-Type Formulas
On the recollection that is made on the surface of the CAPM formula. The security of the market needs to be very superficially intact. Hence, there is a prominent need to get the assurance of a capital bunch. E(˜ri) = rF + [E(˜rM) −rF] . βi – this is such a formula that determines the total idea of the work that is well done. As referred in the risk taking factor of it.
At a very initial glance, you might be able to locate the source of variations that are infused with the composition.
The very first assumption that you make is by assuming that there is a direct solution that you can avail at any moment. The CAPM formula that you use Is just a very calm and definite calculation that is needed. With the potential to create a very casual way of movement, you too can get a correct assumption. The MVE value rate that you get a glance at is nothing but just a singular distinguish.
Single evaluation that you make is just a random thing that you need to make a sacrifice at. There is a definite need that is persistent. Hence, when you get to catch a glance of the predicting rate of return that is made, you should understand how important it is.
On calculating the value with an extremely tangible amount, you will get a good grip on the subject matter.
The reward that you get for the tangent value, that you get is based on the CAPM formula. Hence when the work is adapted, there is a great change in the terms and the notifications that you receive.
The right rate of such a batch would be represented as, OK
The security value that is infused with the value of the formula gives a good explanation to the queries. The security that is added with the beta value makes the portfolio that is made an impactful article. The measurement that is obtained is the perfect risk eliminating factor. And hence, you can get the definition.
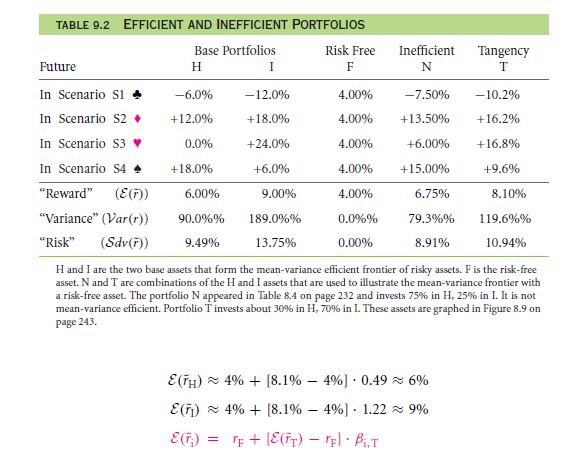
Take a good look at the table 9.2; what you are going to get a hold is that there is a good security rate of return that you get into. The relationship is based on the main variations of the security values. The value estimation that you get in the better selling rates makes up for the best parts. Be the tough calculations or easy theories, there is a main factorization that goes on when you want to choose among the series of factors.
The portfolio that you land on without any risks, the case that you are handed along with the variation is nothing other than the cost eliminating value. There is a need for a good looking value and this is given off by the calculation of CAPM.
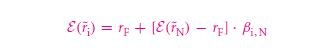The security assurance that you get for the beta value, you get yet answer to be of a portfolio value that is, N (βi,N). This is measured by a variation formula,
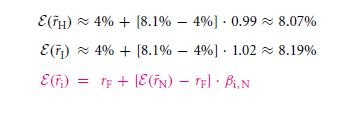In case, you take a close look at the table listed as table 9.2, you can see that the portfolio is offered by the reward that gives the reward value of 6%. It is basically confirmed that the formula of this type does not show the value of only one particular taste.
The portfolio hence does not give a general mean value.
There is no notable involvement of economics at all. The investors will invest no matter what the formulas give.
9.7 C Economics: The CAPM And Its Logic
The previous chapters have discussed this that,
- There is a mean variance that you need to keep a mind open for. This is the basic thing that determines the risks and rewards that you get.
- There is no need for a risk full work at hand and many similar things.
The portfolio value comes in as the value evaluation for the maximizing property. The security that you have in line is made and governed by the basic CAPM value. There is a need for the appropriate incorporation of these values to get a correct market assessment. That is to evaluate any risk before taking the work at hand.
The beauty of a CAPM formula is that you can get an idea of the CAPM value. The CAPM value that you get is used to give the perfect market value and hence even the hurdle rate.
Links of Previous Main Topic:-
- The capital asset pricing model
- What you already know and what you want to know
- The capital asset pricing model capm a cookbook recipe approach
- The capm cost of capital in the present value formula
- Estimating the capm inputs
- Empirical evidence is the capm the right model
- Application certainty equivalence
Links of Next Financial Accounting Topics:-
