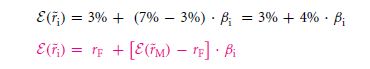CAPM is a certain model which will give anyone the right chance for a certain expected return rate or as we confirmed the cost of capital. This is for every project at hand that you give off for a relevant risk. A model often states the confirming factor that any investment is nothing but a matter with a great cost of capital and a low diverse benefit. Models often make a better list of the diversifying factors that we hold on to. There will be less awkwardness in avoiding such a clueless decision. The markets focus on making a beta distribution which gives a high rate than the one that is expected. With all the projects that continue to be a one of a kind venture, there remain many possibilities that make then much prone to unassisted risks. The expected return rate may even be a very peculiar one with the rate of return being as the exact one that you had wished or longed for. CAPM gives exactly this sort of relationship for you to proudly dive into.
So, now let us go on ahead and use the formula that we just got a hold of. On the account of you believing that the risk free rate is a total of three percent and the main rate that is listed on the return is a total of seven percent, i.e., depending on the stock market, then the approximate CAPM will roll on to be,
In such an extent, if the project that is given to you has the beta value of 0.5, the cost of capital must have a value of 3% + 4% multiplied by 0.5, giving an answer of 5%. A project on the other hand which showcases a beta value of 2 technically must give a cost of capital that is 3% + 4% multiplied by the value 2 giving off a percentage that is 11%.
CAPM further gives a dashing opportunity to the investors on the total cost of capital. Which is, if a project takes on risks, it can actually return the rates to your investor body. As far as the opportunities go on, you can get on to find new group of investors who would handle such opportunities like a pro.
Another name that is given to this model is that of asset pricing model. Even either the expressed taxonomy, the requirement is made on the expected rate of the return rather than the main focused term which gives a righteous term. The price of the project is a fair one in the market and hence fetches a very good value for the CAPM. The expectant cash flow will be that of the one that returns on a discounted rate. The cash flow remains to be almost the right one with two doses of aspirin. The CAPM value otherwise has an uncertain equivalent anomy. Look into the chapter appendix to get a hold of the unadulterated meaning.
CAPM mostly ignores the main standardized deviation rate of return which places a rightly acclaimed price value. This is not because the model poses as a problem, but simply because the risk is just a mild step away. Investors mostly do not care for the projects that face a negative on the beta level in the market. As they measure low on the risk full component. Investors are just busy trying to expand and commemorate the ways to diversify the portfolio in the market.
The many discretions that follow with a personal choice, there are absolutely 3 ways to input the CAPM values. All that you need to do is check on the one rate of return that follows on with future. Not on the session of average learning, the betas that factor into the market of projects, the average rates that are of return fall under the category of firms. As a usual dynamic power between the estimates, you must remember that these are all parts of the data collected from many eras. You will get the idea of what and how anyone can truly estimate the value that needs to be put on in case of a CAPM value input condition. This will be demonstrated in the section 9.4. However, first let us go through the many model numbers that are used to configure the random inputs.
9.2 A The security market line (SML)
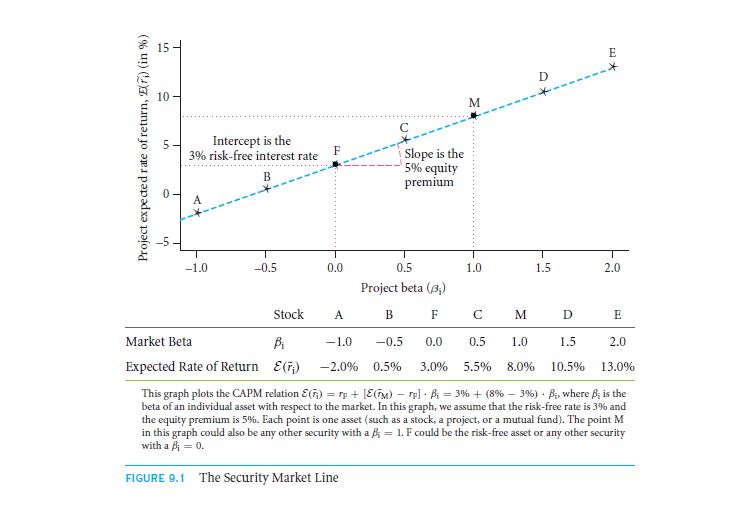
Applying the formula of the CAPM, let us take a look at a specific example. Supposing the risk free rate is calculated to be 3% at a yearly rate. The rate of stock market will be that of the expectant rate of return will be 8% every year. This when incorporated on a stock will read as the CAPM formula with a stock value of beta 1 and it must offer the return rate that is expected of it as 3% + (8% − 3%) * 1 = 8% yearly. In case the stock value is that of beta 0, the expected rate of return will be a 3% + (8% − 3%) * 0 = 3%. This too will be for a yearly fashion. With a stock beta of the value ½, the expectant rate of return will be 3% + (8% − 3%) * 0.5 = 5.5% this will be for a per annum rate too. if for any case the rate of return is to be calculated for a beta of 2, then it would be 3% + (8% − 3%) * 2 = 13% yearly. This goes on and on further.
The formula to be graphed is known widely as a security market line better known as the SML. This graphical representation will get the better of the value that is mostly found among the rate of return and the beta rate. The figure that is displayed in 9.1, marks the even assets and the main security market line.
Every stock that makes up to be a marking point in the façade of the coordinate system, makes it on the diagrammatical representation because the main assets in the formula is used in it. They must lie on a straight line. This is possible to get a hand on as the SML graphical representation is mainly of the CAPM formula. To decipher the meaning of the SML graph that is depicted, you need to understand the equity premium value of the CAPM. The line that intercepts that of the non- risky rate that is used.
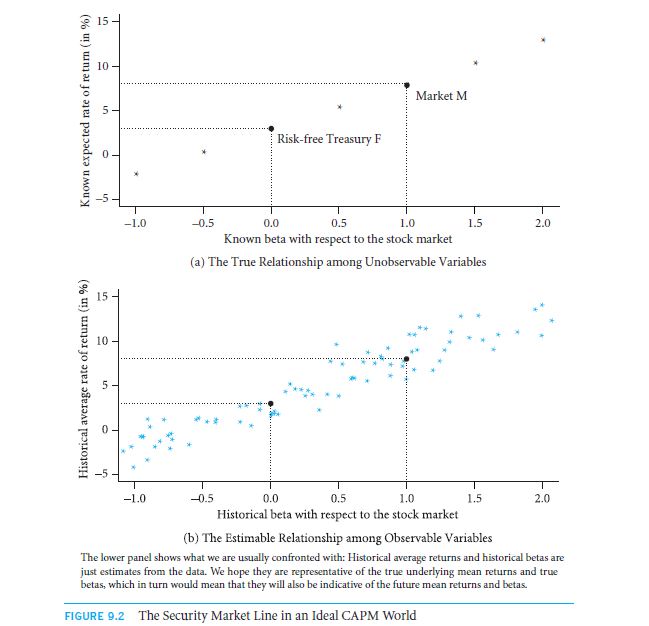
To our dismay, the true world will be having a CAPM rate which is shown in the data that is drawn in the 9.1 figure. Reasons for the expectant return rate are compelling to the market beta. As the figure 9.2 shows, there are 2 graphs in a world that is completely ruled by the CAPM nature. The top portion is repetitive of the input values. That is the true market value figures that are exclusively used to make a premium rate of return. The rate of return that you make use of is something that cannot be truly observed. It forms a complete straight line. The lower portion of the graph cannot focus on the observable qualities. The more prominent data that you get to input is a major one. With the value of the observable qualities that are defined on a graph, you must rely on them. This is a factor only when the graph falls as a very straight line with no deflections.
Only that of an original security market can make the cut and fit in to the distractions. On lying with the presentable hope, the data will mostly provide for a good element of choice. With so many available elements that completely influence the variety, the straightness of the represented line is an unavoidable deal. The relationship that you get to emerge with the investors is displayed by the profit making. On estimating the data value, it is clear that the market is a beta oriented.
Links of Previous Main Topic:-
Links of Next Financial Accounting Topics:-