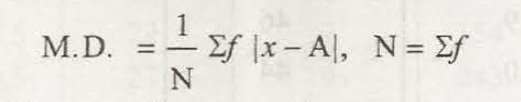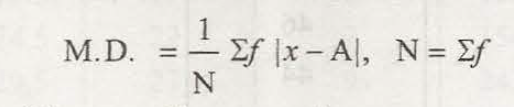The mean deviation is known to be the first measure of dispersion. It is regarded to be absolute difference between different values in set of value and also average is taken of all values of set. It is possible to calculate mean deviation either from median or mean. But at times, median is preferred as the signs are ignored and sum of deviation can be taken from median is minimum.
The formula which is used to calculate mean deviation is defined as:
![]()
Mean deviation from mean = Σǀ X- X̅ ǀ /N
Mean deviation from median = Σǀ X-M ǀ/N
Σ = the sum
X = the observation
X̅ = the mean
N = the number of observation
Drawback related to mean deviation is the use of absolute deviation. The reason behind use of Σǀ X- X̅ ǀ appears to be always equal to zero. Mean deviation is actually based on observation and it is a property that is not possessed by any range or quartile deviation. Through this formula you can certainly get a mathematical impression which is known to be an effective means of measuring variation in data.
Links of Previous Main Topic:-
Links of Next Statistics Topics:-
- Moments
- Bivariate distribution
- Theorem of total probability addition theorem
- Random variable
- Binomial distribution
- What is sampling
- Estimation
- Statistical hypothesis and related terms
- Analysis of variance introduction
- Definition of stochastic process
- Introduction operations research
- Introduction and mathematical formulation in transportation problems
- Introduction and mathematical formulation
- Queuing theory introduction
- Inventory control introduction
- Simulation introduction
- Time calculations in network
- Introduction of game theory