Here we will fist come to ɳ HE = W net / Q1 = Q1 –Q2 / Q1 = 1 – Q2 / Q1 which we already have.
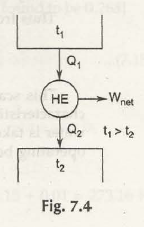
Now consider the figure below:
Firstly as we know t1> t2
so t1 – t2> 0 ( must be for heat flow)
We know reversible heat engine’s efficiency depends on source and sink temperatures.
From there we are at ɳ rev = /1 (t1, t2) where f 1 is a function of t1 and t2
From(7.7)
1 –Q2 / Q1 = f1( t1 , t2)
Either Q2 / Q1 = 1 – F1( T1, T2)
Or, Q1 / Q2 = 1 / 1- f ( t1 , t2) = f2 ( t1,t2)
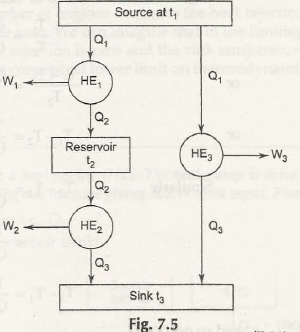
Let us now take three heat engines arranged as shown in Fig. 7.5
Q2 / Q3 = f3( t2 ,t3)
And then Q1 / Q3 = f4( t1 , t3)
Now check out the figure below:
From there you are getting again,
Q1 / Q2 = Q1 / Q3 / Q2/Q3
= f4(t1,t3) / f3 (t2,t3)
or f2 ( t1,t2) = f4 ( t1,t3 / f3 ( t2 , t3)
Now t 1, t2, t3 are independent and t3 does not affect the operation of HE1 which is
operating between t1 and t2.
To satisfy equation (7.11), we must have
And f4( t1,t3) = ϕ (t1) / ϕ(t3)
andf3(t2,t3) = ϕ( t1) / ϕ(t2) = Q1 / Q2
Since ϕ (t) is an arbitrary function, the simplest possible way to define absolute
Thermodynamic temperature Tis to let <j>(t) = T, proposed by Kelvin.
Thus from equation (7.12), we have
Q1 / Q2 = T1/T2
Kelvin scale and the feature:
This is particularly called Kelvin scale. The independent quality from any substance is its unique feature.
In Kelvin scale, the triple point of water is taken as the standard reference point. For a Carnot engine operating between T and T tr (triple point of water), we have
Q /Q tr = T / T tr
T tr = 273.16 k (arbitrary assigned value)
T=273.16 Q / Q tr
If T changes, Q also changes. Thus Q plays an important role of thermodynamic property.
Fig. 7.7 shows a series of heat engines.
T1 / T2 = Q1 / Q2
T1-T2 / T2 = Q1 – Q2 / Q2
T1 –T2 / T2 = Q1 – Q2 / Q2
T1 –T2 = T2 / Q2( Q1 –Q2)
Similarly, T2 – T3 = T3 / Q3( Q2 –Q3)
= T2 / Q2( Q2 – Q3)
T3 – T4 = T2 / Q2( Q3 –Q4)
And so on.
Let W1 = W2 = W3 =… = W
Q1 –Q2 = Q2 – Q3 = Q3 –Q4
Thus, T1 – T2 = ( T2 –T3) = ( T3 –T4) =….(7.16)
Also if it is assumed Q1 – Q2 = Q2 – Q3 = Q3 – Q4 = …
Then also W1 = W2 = W3 = … = W
Equation (7.16) shows equal temperature intervals usually steam point and ice point are taken as fixed reference temperatures and the difference between the two is arbitrary taken as 100°C.
TS – Ti =100 , [TS = steam point Ti = ice point]
ɳ rev = 1 – Ti / TS= 0.268 [ ɳrev measured and found to be 0.268]
Ti / TS = 0.732
(7.17) =>TS – 0.732 ts = 100
Ts = 100 / 0.268 = 373.15 ( steam point)
Ti = 273.15 (ice point)
Triple point of water is at 0.01°C. For this in Kelvin scale 273.15 + 0.01 = 273.16 K.
Links of Previous Main Topic:-
- Statement of zeroth law of thermodynamics with explanation
- Heat and work introduction
- Open system and control volume
- Conversion of work into heat
- Introduction to carnot cycle
- Efficiency of carnot cycle
- Carnots theorem
Links of Next Mechanical Engineering Topics:-
- Absolute zero on thermodynamic temperature scale
- Clausius inequality entropy and irreversibility introduction
- Ideal gas or perfect gas
- Introduction about air standard cycles
- Properties of pure substances introduction
- Vapour compression refrigeration cycle introduction
- Basic fluid mechanics and properties of fluids introduction