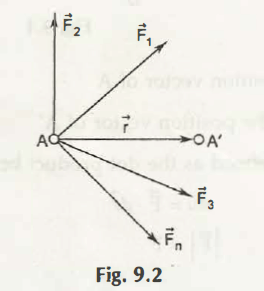
Let us consider a particle A displaces to A’ due to several external forces F1, F2, F3….. Fn. This imagined displacement to become A’ is virtual displacement as shown in Fig. 9.2
Then, virtual work can be given by-
u = F1.r + F2.r + F3.r +……+ Fn.r
= (F1+ F2 + F3 +……+ Fn)r
= R.r
Where,
R = Resultant of all the forces
Or,
It can be defined as sum of virtual work of every single force is equal to its resultant.
Suppose the body is in equilibrium while applying the force. In this condition, the resultant R will be equal to 0 (zero).
The above statement helps in defining the principle of virtual work. It states that total virtual work of forces will be zero for any displacement when the body is in equilibrium.
Links of Previous Main Topic:-
- Introduction concept of equilibrium of rigid body
- Friction introduction
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Sign convention of mechanical work
Links of Next Mechanical Engineering Topics:-