Different parts of a reciprocating engine is shown in Fig. 4.4 (a)
Let us consider this figure,
Point A will have linear motion towards point C along the line AC
Point B will have circular motion with an angular velocity
Thus,
Velocity at point A, VA = 0 AO
Similarly,
Velocity at point B, VB = C0 BO
Or,
r = 0 BO. 0r/ BO
VA = 0 AO
= (r) AO/ BO
Hence,
We can easily get the velocity at point A by knowing the values of all elements.
Analytical Method to find VA
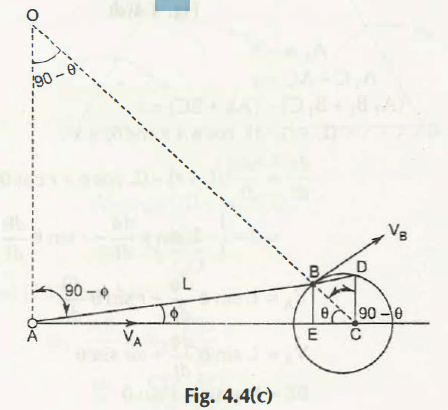
Fig. 4.4 (c) shows the graphical representation of different parts of an engine.
To find the velocity at point A, we can use different analytical methods.
Method 1:
Draw line CD ⏊ AC and line BE ⏊ AC
Now,
In AOB and BCD
⦟AOB = 900 – = ⦟BCD
⦟OAB = 900 – = ⦟BDC (we know that ⦟OBA = ⦟LCB)
Hence,
AO/ BO = CD/ BC = CD/ r
And,
tan = CD/ AC
CD = AC. tan
= (AE + EC) tan
= (L cos + r cos ) tan
= L sin + r cos tan
Since,
VA = (r) AO/ BO
= (r) CD/ r
= (L sin + r cos tan)
Method 2:
Suppose the crank is at IDC (Inner Death Centre). In this condition,
A1B1 = AB = L
B1C = r
Hence,
AO/ BO = CD/ BC = CD/ r
tan = CD/ AC
we know that
CD = AC. tan
= (AE + EC) tan
= (L cos + r cos ) tan
= L sin + r cos tan
Thus,
VA = (r) AO/ BO
= (r) CD/ r
= (L sin + r cos tan)
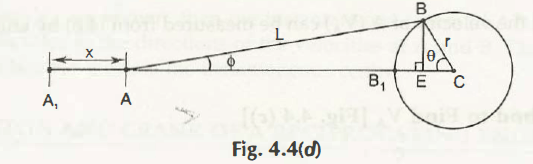
Method 3:
Considering the Fig.4.4 (d),
Let, A1A be x
It can be written as,
A1C – AC = x
(A1B1 + B1C) – (AE + EC) = x
(L + r) – (L cos + r cos ) = x
Differentiating the above equation with respect to time, we get-
=
= L sin+ r sin
Hence,
VA = L sin+ r sin
Since,
BE = L sin = r sin
sin = r/ L sin
Differentiating the above equation with respect to time, we get-
cos =r/ L
= r/ L cos
= rcos / Lcos
Now, substitute this value to get VA,
Therefore velocity at point A,
VA = L sin(rcos / Lcos ) + r sin
= r cos sincos + r sin
= (L sin + r cos tan)
Links of Previous Main Topic:-
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Position vector velocity and acceleration
- Plane kinematics of rigid bodies introduction
- Combined motion of translation and rotation
- Instantaneous centre of rotation method
Links of Next Mechanical Engineering Topics:-