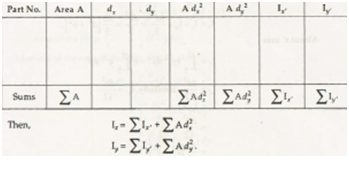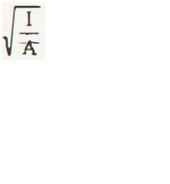Summation of moment of inertia of components of composite plane figures about an axis is known as moment of inertia of that composite figure about the same axis. The value of components of composite figure can be positive or negative.
Suppose we have all components parts as positive so it will be added to give certain bigger value for the determination of moment of inertia. In case, some of the components are negative. The values will be taken as it is. The value of final result will be the summation of positive and negative values.
A table has been made for the purpose of calculation as given below-
If K be the radius of gyration for the given composite figure, then its value can be written as-
K =
Parallel Axis Theorem for Moment of Inertia
We know that moment of inertia of an object can be determined by the summation of components of the object. But when the case is different and we have to calculate moment of inertia, we can use Parallel Axis Theorem.
For example:
Take the case of T-beam to determine moment of inertia. We have to divide the whole section into small rectangles and consider the centroidal axis of each rectangle as reference axis for the rectangle so that we can determine moment of inertia of separate rectangles.
After finding these values, the moment of inertia of T-beam can be given by the summation of values determined for each individual rectangle. This is called the Parallel Axis Theorem.
Links of Previous Main Topic:-
- Introduction to statics
- Introduction to vector algebra
- Introduction concept of equilibrium of rigid body
- Friction introduction
- Area moments of inertia in rectangular and polar coordinates
- Radius of gyration
Links of Next Mechanical Engineering Topics:-