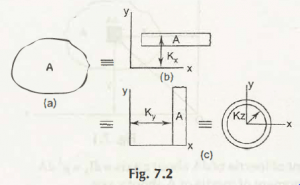
Suppose the area A of lamina is converted into long narrow strip of same area A as shown in Fig. 7.2
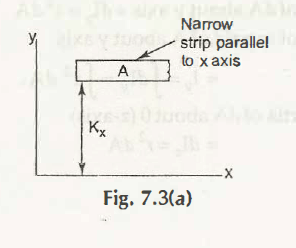
Considering its rectangular coordinate as (x, y), shown in Fig. 7.3 (a)
Now, moment of inertia of long narrow strip can be written as-
For x-axis (parallel to x-axis),
Ix = Kx2 A
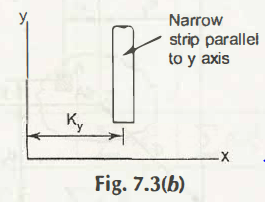
In Fig. 7.3 (b),
Now, moment of inertia of long narrow strip can be written as-
For y-axis (parallel to y-axis),
Iy = Ky2A
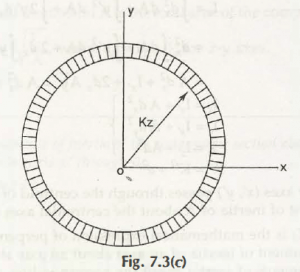
In Fig. 7.3 (c),
We get,
dIx = (dx + y’)2dA
= dx2dA + y’2dA + 2y’ dxdA
Now,
Ix = x2dA + ’2dA + y’ dxdA
= dx2A + ’2dA + 2dx’dA
= A dx2 + Ix’ + 2dx A
= A dx2 + Ix’
Similarly,
For y-axis, we get-
Iy = A dy2 + Iy’
For z-axis, we get-
Iz = A dz2 + Iz’
Thus, it can be written as-
K2 = K2 + d2
Note:
Hence, the axes (x’, y’) passes through centroid of axes (x’, y’, z’) of area A.
Equation 7.2 defines the perpendicular axis theoremthat states, area moment of inertia about an axis at origin and normal to plane (x and y) is the sum of area moment of inertia about the corresponding x-axis and y-axis.
Equation 7.5 defines the parallel axis theorem that states, when area moment of inertia of plane passes through centroid, area moment of inertia of narrow circular ring is given by,
Iz = Kz2 A
Similarly, we get-
Ix = Kx2 A or, Kx =
Iy = Ky2 A or, Ky =
Iz = Kz2 A or, Kz =
Since,
Iz = Ix + Iy
Hence,
Kz2 A = Kx2 A + Ky2 A
Kz2 = Kx2 + Ky2
Links of Previous Main Topic:-
- Introduction to statics
- Introduction to vector algebra
- Introduction concept of equilibrium of rigid body
- Friction introduction
- Area moments of inertia in rectangular and polar coordinates
- Radius of gyration
Links of Next Mechanical Engineering Topics:-