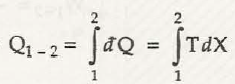The quantity of heat transferred not only depends on the state of the object at the end, but it also depends on the path followed by it. Thus heat transfer can also be called a path function. Thus Q can be written as heat transfer.
Therefore it is an in accurate differential.
So uneven temperature or the imbalance of heat enhances the transfer the transfer of heat. To be moreevident the difference in temperature causes the heat to flow between the bodies until equilibrium is attained.
Thus heat transfer is mathematically represented by
where T=intensive property and X = extensive property of the substance.
It is applicable only for a quasi-static process only. The quantity of heatbeing transferred can be calculated from the area under (T, X) coordinates illustration
dQ = T dX
dX =dQ / T
Hereone / T is an integrating factor which is used with inaccurate quantity to create it precisedifferences.
Solved Examples
Example 3.1- Centrifugal pump powers up water horizontally at two m3/min from an open well to a closed tank. The pressure here is 0.45 Mpa. So calculate the work of the pump which it must do to the water in an hour just to strength the water into the tank contrary to the pressure.
Solution. P = 0.45 x 106 Pa = 450 kPa
dV = 2m3 , time , t = 1 min
= V2 – V1
In one minute work done = ʃ = pd V = P ( V2-V1)
= 450 (2-0) = 900 kNm.
Thus in one hour, the work was done= 900 x 60 KJ / hr.
= 54000 KJ/hr.
Example 3.2. A petrol engine cylinder is fitted with a piston of aplane at 0.15 m2 and maintaining its pressure at 2MPa. Thus the gas increasesby a straight line process on the P – V diagram. Therefore the last pressure remains 0.2 Mpa. NowAnalyse the work done by the gas on the piston if the stroke is 0.15 m.
Solution
WI-2 = area under the curve (Straight line) 1-2
= 1/2 [ 2 + 0.2] x 106 x 0.15 x 0.15 Nm
= 24.75 KJ. Ans.
Example 3.3 – If a mass of 2 kg of air is trampled in a quasi-static process from 0.15 Mpa to 0.75 Mpa for which PV = Const.Then find out the initial density of air which is 1.5 kg/m3. Also, determinethe work done by the piston to compress the air.
Solution. We have W1 2 = P1 V1 In P1 / P2
= 0.15
= – 0.15 x 106 x 2 / 1.5 In 0.15 / 0.75 J
= – 0.321888 x 106 J
= – 321.8 KJ
The negative sign of work confirmations that the work is done on the system.
Example 3.4- A certain amount of gas is trampled in a quasi-equilibrium process from 90 KPa,0.15 m3 to 0.5 MPa, 0.04 m3. Now let us consider that the pressure and volume are connected by PV” =Canst. So determine the work done on the gas system. (Take n = 1.3)
Solution
W1 = P1 V1 – P2 –P2 / n-1 = 90 x 103 x 0.15 – 0.5 x 106 x 0.04 J / 1,3 – 1
= – 21.7 Kj.
Negative sign shows that the work is done on the system.
Example 3.5– Analyze the total work done by a gas system in a expansion process shown in
Fig. 3.12 (1 bar = Uf N/m2)
Solution
W1-2-3 = W1-2 + W2-3
Now W1-2 = 50 x 105 x (0.4 -0.2 ) J = 10 x 105 J [ Note.P1V2 = P3 V3]
W2-3 = P2 V2-P3 V3 / n-1 = P2 V2 / n-1 [ 1 – (P3 / P2) n-1 / n
=P2 V2 / n-1 [ 1 – ( V2 / V3) n-1]
= 50 x105 x 0.4 / 13.1 [ 1- (0.4 / 0.8)0.3]
= 12.516 x 105 J
= 2.2156 x 106 J = 2.2516 MJ. Ans.
Links of Previous Main Topic:-
- Simple stress introduction
- Normal strain
- Statically indeterminate system
- Introduction to thermodynamics
- Statement of zeroth law of thermodynamics with explanation
- Heat and work introduction
- 3 2 1 concept of work in mechanics
- Work done in a quasi static path
- 3 4 2 convention of sign of heat
Links of Next Mechanical Engineering Topics:-