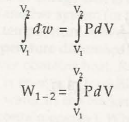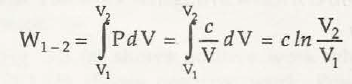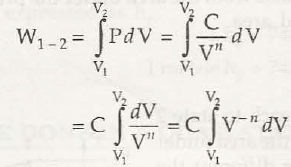Let us assume that a cylinder fitted with a piston as some gas mechanism as shown in the figure given below Fig. 3.4 (a).Thus the gas is in equilibrium under a provided thermodynamic condition at the piston 1. This is described by P1 and V1 at pressure P1. Now after the movement of te piston it comes in position 2 which is also at equilibrium state which is denoted by P2 and V2.
It is also worth mentioning that any stage inbetween is also in equilibrium. The piston can also move at any point which has a distance dl. So if we considerA as the area of the cross-section of the cylinder, then the volume evacuated is AdZ = dV. Therefore the small work done is F.dl.
dW =f.dl = PAdl = PdV
Therefore the volume diverges from V1 to V2. Therefore the total work done is given by
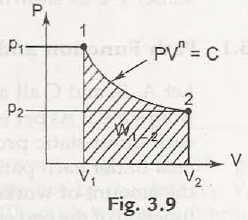
So now we can calculate the magnitude of work from the area under the process (quasistatic) as represented in Fig. 3.4 (b) by shaded area.
3.3.1 Path Function and Point Function
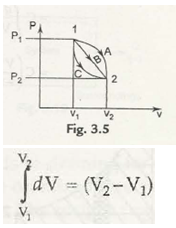
Let us assume A, B, and C all as the quasi-static trails to transform fro one state to another state. Now according to the equation (3.1), work is explained as the range of each quasi-static process. Now due to the difference in the paths, the area under each path becomes different. Therefore it is concludedthat the amount of workdonein each process is not the only the functions of the end states of the process, butit is also influenced by the path that when transforming from one state to another. These are the causes why work is called a path function or an inexact differentialmathematically. Just because of the fixed point in thermodynamic properties the state present in the in the diagram (Fig. 3.5) is called point function. The discrepancies of point features are precise differentials, and the mixing is simple.
Thus we can also roughly estimateV1 is the volume at 1, V2 is the volume at 2, and the alteration insizecan be determined by only on the initial and final states.
PdV Work in Various Quasi-Static Processes
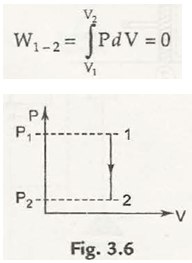
(a) Constant volume process : Here V = Const.
Thus , dV = 0 , so
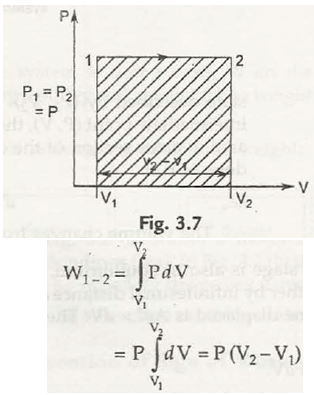
(b) Constant pressure process : Here P = Const. so we can take out P from integration.
(c) Process in which PV =canst. = c.
or , w1 -2 = p1V1 In V2 / V1 = P1V1 In P1 / P2
(d) Process in which PV” = Const. = C
C = (V –n+1/ -n +1) v1v2 = C / 1-n [V12 – V1-n]
= 1 / 1-n [ CV1-n 2 – CV 1-n 1 ]
= 1/ 1-n [ P2 V2 V1 – P1 V1 V1-n]
W1-2 = 1 / 1-n [ P2 V2 – P1 V1]
= P1V1 – P2 V2 / n -1 = P1 V1 /n-1 [ 1-(P2 P1) n-1 / n
If the system is having ideal gas, then we have
P1 V1 / T1 = P2 V2 / T2
We get T2 / T1 = P2 V2 / P1 V1 = ( P2 / P1 ) n-1 /n = ( V1 / V2) n-1
W1-2 =mR (T2 –T1 / 1-n) , [ P2 V2 = mRT2 , P1 V1 = mRT1 ]
Links of Previous Main Topic:-
- Simple stress introduction
- Normal strain
- Statically indeterminate system
- Introduction to thermodynamics
- Statement of zeroth law of thermodynamics with explanation
- Heat and work introduction
- 3 2 1 concept of work in mechanics
Links of Next Mechanical Engineering Topics:-