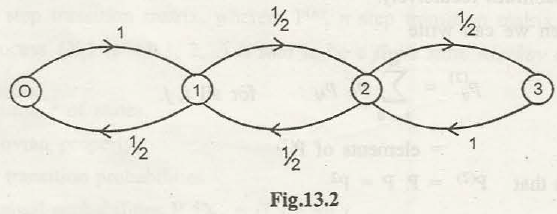
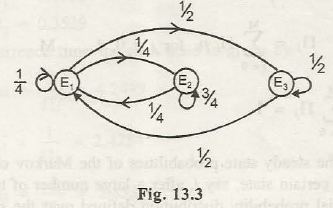
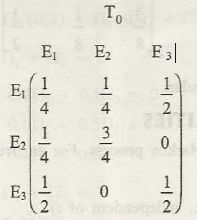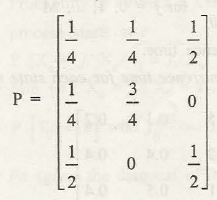Various kinds of states and transitions seem to occur in Markov chain that needs to be known. We shall discuss some of the most important kind of states:
- Recurrent state:
In first kind of state probability is defined as 1 because the process returns back to the initial place from where it started after a number of transition. This type of state is known as recurrent state.
- Transient state:
Next type of state is known as transient state in which the process may or may not return back to its initial position i.e. it may not recur like the recurring state.
- There is two cases of recurrent state:
- If the average time to return back to the initial position is known and is finite then the state is known as recurrent and non-null.
- Next case is if the average time of returning back to the initial position is known but infinite then the state is known as recurrent and null.
- Aperiodic state:
Next type of state is known as aperiodic state if for a number say L, then there is some method to return to the number L, L+1, …..∞ Transitions.
- Periodic state:
The reverse of aperiodic state is known as periodic state.
Some properties of Markov chain depending on the above type of states:
- It there is a way to reach all the states from various other state then it is said that Markov chain is irreducible.
- The Markov chain can be transient if all states are transient. Similarly it can be recurrent non-null, recurrent null, aperiodic and periodic if all the state is also has the same property.
- Ergodic Markov chain: in this case the chain should satisfy the property of irreducible, non-null and aperiodic.
It is said that in Ergodic case you can reach any other state within a fixed number of steps irrespective of the initial position. There is a chain called regular chain that goes side by side with ergodic chain. Thus it is seen that regular chain should always be ergodic but the inverse is not true.
Links of Previous Main Topic:-
- Introduction to statistics
- Knowledge of central tendency or location
- Definition of dispersion
- Moments
- Bivariate distribution
- Theorem of total probability addition theorem
- Random variable
- Binomial distribution
- What is sampling
- Estimation
- Statistical hypothesis and related terms
- Analysis of variance introduction
- Definition of stochastic process
- Definition of stochastic process
- Markov process and markov chain
Links of Next Statistics Topics:-
- Introduction operations research
- Introduction and mathematical formulation in transportation problems
- Introduction and mathematical formulation
- Queuing theory introduction
- Inventory control introduction
- Simulation introduction
- Time calculations in network
- Introduction of game theory
- Steady state probabilities
- Entrance probability theorem