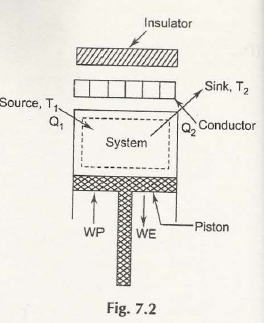
For grabbing the complete view on the working of Carnot cycle consider this figure:
In the first state, you will have to measure initial volume and pressure of the mass syste, here 1 kg mass in particular in the cylinder.
The head of the cylinder will work as heat conductor and both q1 and quantity of heat and T1 or temperature is delivered to that context until the cylinder will reach its stage 2. When the volume will expand you’ll find isothermal expansion process 1 – 2. At stage 2 heat supply will be stopped.
For process 1 – 2 we apply 1st law,
q1-2= u2 – u1+Wt-2
[u2 – u1 = 0 for isothermal process]
= O+wt-2
Or q1 = p1v1
In v2 / v1 = RT1 In v2 / v1
w1 -2 is the work done by the system. It is positive (v2> v1).
In stage two cylinder head will now work as an insulator and the process of 2 – 3 will manipulate heat supply to cut off. You will again find the whole system expanding and reversing adiabatically and a fall in its temperature, here to T2.
For process 2 – 3
q2 -3 = u3– u2 + w2- 3
0= u3-u2+Wz-J
W2-3= (u2-u3)
Work w2-3 is done by the system at the expense or decrease in internal energy.
In stage 3, cylinder head is transformed to conductor. A volume of heat here q2 will come out and sink and the temperature will remain constant, here T2. You will face 3 – 4 and again isothermal heat rejection process.
q3-4= u4-u3+w3-4
or q2-0 +w3-4 = P3 v3 In u4 / u4
This w3 – 4 is done on the system. … (7.2)
In stage 4 the cylinder head will behave as an insulator once again and a situation of adiabatic compression will come forward ultimately reaching stage one and completing that cycle.
q4- 1 = u1 – U4 + W4 -1
0=u1-U4+W4-l
or W4-1=u4-u1.
Links of Previous Main Topic:-
- Statement of zeroth law of thermodynamics with explanation
- Heat and work introduction
- Open system and control volume
- Conversion of work into heat
- Introduction to carnot cycle
Links of Next Mechanical Engineering Topics:-
- Efficiency of carnot cycle
- Carnots theorem
- Absolute thermodynamic temperature scale or kelvin scale
- Absolute zero on thermodynamic temperature scale
- Clausius inequality entropy and irreversibility introduction
- Ideal gas or perfect gas
- Introduction about air standard cycles
- Properties of pure substances introduction
- Vapour compression refrigeration cycle introduction
- Basic fluid mechanics and properties of fluids introduction