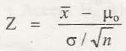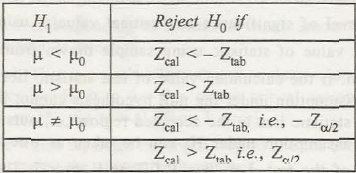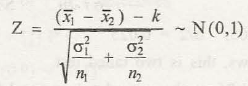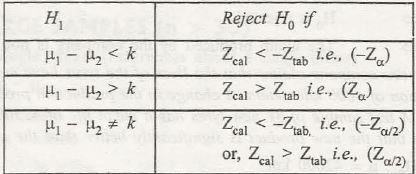Tests for Large Samples
In case of financing there is a specific test for large samples that is used to get detailed idea of the calculation process. To find the population mean, there are specifically 2 formulas that can be used in testing the hypotheses that is framed for a population taking tests with large samples in consideration.
While dealing with test samples, it is specifically standard deviation method that is followed. It is either the population standard deviation method or sample standard deviation method that is used.
The primary factors in this case- To understand how to apply this step by step procedure as you consider population mean that has a large sample size.
Also, how this test result is interpreted against the original content.
- Conclusion of a single mean (testing related to a single mean)
Initially, the set up for H0 should be µ = µ0
For the set up for H1,
- (µ ≠ µ0)
- (µ < µ)
- Or it would be (µ > µ0)
Set up for the test statistics that will be following normal distribution in standard level is depicted via,
Its critical value will be set up as Ztaband ‘a’ is used for depicting the level of significance.
The next step highlights the computation of Ztab(based on assumption)
Its decision is based on calculations which are provided in given table below,
For instance, in a large sample if ‘σ’ or population S.D is unknown, then in the test statistic, asample of S.D can be taken.
- Dual means or 2 means: Testing their differences
Let us assume the fact that there are 2 populated bodies having different means. If we consider their variances as ‘σ12’ and ‘σ22’,and their means as ‘µ1’ and ‘µ2’; then set up for H0 can be taken as µ1 – µ2. The resultant for this equation is ‘k.’
On setting up the calculation for H1,
- µ1 and µ2< k
- µ1 and µ2> k
- µ1 and µ2≠ k
In all these cases, ‘k’ is taken as a specified constant.
After setting up the statistics, the equation stands to be as,
Here,
- k = constant
- n1 = sample size of first population
- n2 = sample size of second population
- X2 = means of n2
- X1 = means of n1
In this case too, the critical value is taken as Ztaband level of significance is assumed as ‘a.’
After calculating the critical value (say Zcal)as per the statistics, its final answers as per the decisions stated in the provided table showcases,
Estimation of population S.D can be made when n1 and n2 > or = 30.
Links of Previous Main Topic:-
- Introduction to statistics
- Knowledge of central tendency or location
- Definition of dispersion
- Moments
- Bivariate distribution
- Theorem of total probability addition theorem
- Random variable
- Binomial distribution
- What is sampling
- Estimation
Links of Next Statistics Topics:-
- Statistical hypothesis and related terms
- Analysis of variance introduction
- Definition of stochastic process
- Introduction operations research
- Introduction and mathematical formulation in transportation problems
- Introduction and mathematical formulation
- Queuing theory introduction
- Inventory control introduction
- Simulation introduction
- Time calculations in network
- Introduction of game theory