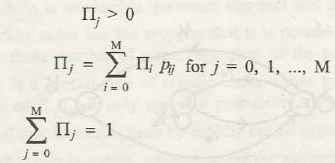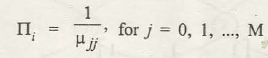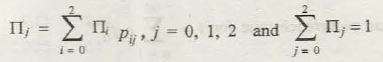There is a long run expression of Markov process which is known as steady-state probabilities which shows thatwhen the sample of a Markov chain cannot be reduced further. It is shown by:
Lt pij(n) = ∏j (i.e., independent of i)
Where ∏j shows the steady state and is denoted by the equation:
In the above expression we see that ∏j is the steady state because in the process of finding a probability of a state say j, in the long run the transition slowly tends to return back to ∏j .
We also have an equation as:
µijstands for expected recurrence time. This shows the mean recurrence time of each state.
Links of Previous Main Topic:-
- Introduction to statistics
- Knowledge of central tendency or location
- Definition of dispersion
- Moments
- Bivariate distribution
- Theorem of total probability addition theorem
- Random variable
- Binomial distribution
- What is sampling
- Estimation
- Statistical hypothesis and related terms
- Analysis of variance introduction
- Definition of stochastic process
Links of Next Statistics Topics:-