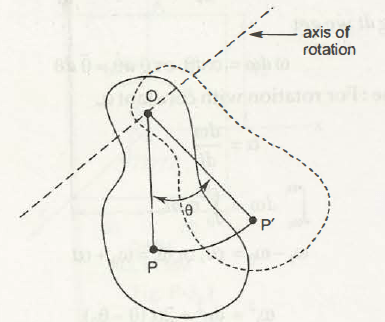
Let us consider a rigid body rotates about any fixed axis whose particles follow circular path. In this condition, the particles of the rigid body possess zero velocity and zero acceleration on this fixed axis of rotation as shown in Fig. 3.2 (a),
Considering the Fig. 3.2 (b), it shows the angular positions of two lines
From the above figure, we can write-
1 – 2 =
As angle is for rigid body motion, it cannot be changed. So its differentiation w.r.t time is zero, i.e.,
1 – 2 = 0
or,
1=2
This implies that change in angular displacement will remain same for all lines on the rigid body. Similarly, the angular velocity and angular acceleration will also be same.
Links of Previous Main Topic:-
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Position vector velocity and acceleration
- Plane kinematics of rigid bodies introduction
- Translation
Links of Next Mechanical Engineering Topics:-