The kinetic theory of gases:
We already know of Pv = RT which is the ideal state of gas. This is called the kinetic theory of gas. There are certain facts that are important in this theory:
- In the molecules of the gas there is neither attraction nor repulsion.
- Molecules and there volumes are totally overwhelmed by the gas and its volume.
- Molecules in the gas are totally flexible; they can behave elastic and also rigid. This is why there is no loss of momentum when these molecules crash with each other or with the walls where they are kept.
- You will find similar behavior of the real gas with the ideal gas when the pressure is low and temperature is very high.
- But as pressure increases the point (c) is no longer valid. The inter molecular forces of attraction or repulsion increases, and also the point (b) are invalid.
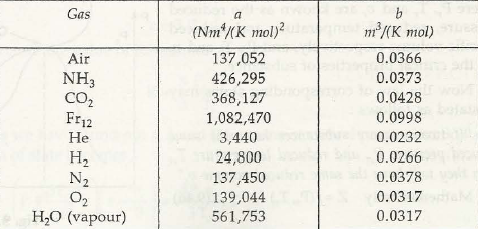
For real gas the following equations are valid.
- ( p + a / u2) ( u-b) = RT à van der waal’s equation where (a / v2 ) takes into account for intermolecular forces of attraction and b is calledco volume taking account for volumes of molecules.
- p = RT / u-b – a / T u2 à bethelot’s equation
- Dieterici’s equation
- Redlich-Kwong’s equation
- Saha-Bose equation
- p = RT ( 1-e) / u2 ( u +B) – A /u2 àBeatlie-Bridgeman equation
Where A = A0 ( 1- a / u) , B = B0 ( 1- b /u) , e = C / uT3
A0, B0, a, b, c are constants.
Links of Previous Main Topic:-
- Open system and control volume
- Conversion of work into heat
- Introduction to carnot cycle
- Clausius inequality entropy and irreversibility introduction
- Ideal gas or perfect gas
- Ideal gas or perfect gas
- Specific heats internal energy and enthalpy of an ideal gas
- Entropy change of an ideal gas
- Reversible adiabatic process
- P v and t s diagrams for pv c
Links of Next Mechanical Engineering Topics:-