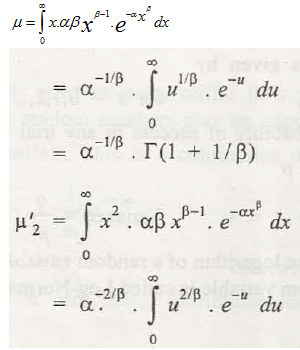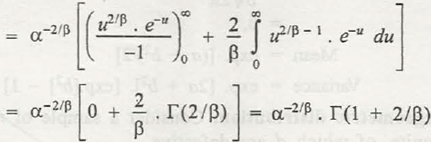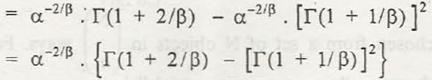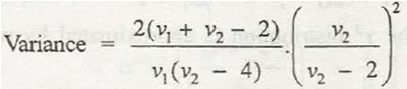Other Distributions

(a) Uniform distribution. Uniform distribution can also be called as continuous distribution or rectangular distribution. The pdf is represented by

f(x)= 1/ (b-a)

a < x < b

= 0,

Here a and b are two constraints.

Mean = (b+a)/2, variance= (b-a)²/12

This distribution is extensively used in variousmovement flow problems and probabilistic inventory problems. Also (0,1) or (a, b) random numbers performs asignificant role in simulation.

 

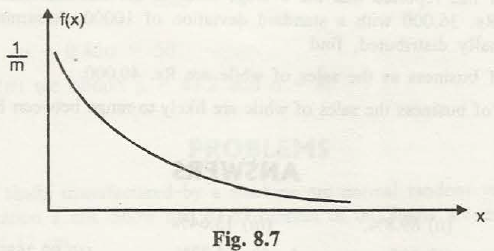
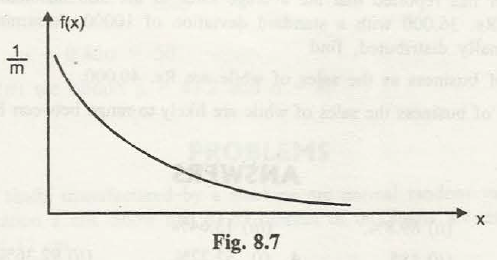
(b) Exponential distribution.This is a continuous distribution, and the pdf is given by

F(x)=1/m. e ^–x/m

=0

x> 0, m > 0

Otherwise

Here m is the parameter. This is a very advantageous distribution for the theory and will be furthermore discussed in Part B.

Mean = m, Variance = m².

 

(c) Gamma distribution. This is also another continuous distribution and the pdf is represented like,

f(x) = 1/ b^a√a.x ^a-1. e^-x/b

x > 0, a > 0, b > 0

=0                                 otherwise

Here, √a= gamma

a and b are the variables. Conditional on the values of these variables we acquirenumerousforms of the gamma distribution.

 

Mean = ab    and          Variance = ab2

 

When a = 1, we catch exponential distribution.

 

(d) Beta distribution– This is also another continuous distribution and the pdf is prearranged by

f(x)=√a+b/√a.√b. x^a-1(1-x)^b-1

,     0 <x< 1, a> 0, b > 0

= 0,   otherwise

Similarly herea and b are two variables of the concerned distribution. When a = 1 and b = 1, we achieve the uniform distribution in the interval (0, 1).

Mean = a/ (a+b),

Variance= ab/ (a+b)²(a+b+1)

 

(e) Geometric distribution. One of the discrete distribution type. The chance of receiving the first attainment on the (x + 1 )^th trial is expressed by

P(x) = pcf, for x = 0, 1, 2,…

Where, p = Probability of success in any trial

q = 1- p

Mean= q/p and variance= q/p²

 

(j) Log-Normal distribution. If the logarithm of any random variable representsageneral distribution, then the distribution assumed by the random variable can be known as Log-Normal distribution. Its probability density function will be expressed as:

f(x)= 1/b√2π.x^-1.exp [-(ln x-a)²/ 2b²], x>0, b>0

= 0,                       otherwise

Mean = exp. [(a + b²)/2]

Variance = exp. [2a + b²]. [exp.[b²] – 1]

 

(g) Hypergeometric distribution. Let us assume a sample of n units to be taken out from a package of containing N units, of which d are defective.

Therefore the x attainments of the defective samples and n – x failures can be selected in (^d _x) (^N-d_n-x)   ways.

Also, n items can be chosen from a set of N objects in (^N n) ways.

For packaging without replacement is the probability of getting “x successes in n trials” is

p (x, n, d, N) =(^d _x) (^N-d_n-x)  / (^N _n)       for x = 0, 1, … , n

Mean= n. d/N

Variance= n.d.(N-d).(N-n)/N².(N-1)

This distribution approaches to binomial with p = d/N when N ->∞ .

 

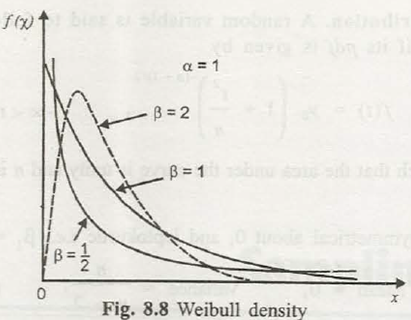
(h) Weibull distribution. This is the other mostimperative distribution that is used in consistency and life testing of an item. The probability density function is represented by

Where, α and β are two variables of the distribution.

Using integration by parts,

So the for this expression will be,

Variance µ₂ = µ’₂ – (Mean)²

 

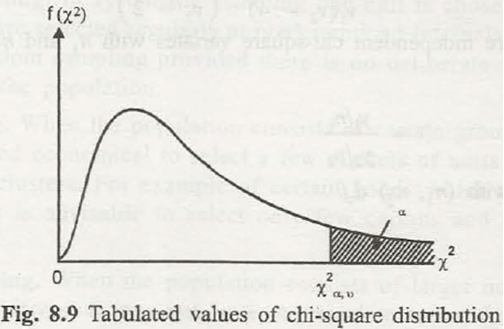
(i) Chi-Square (X² ) distribution- weconsider a variable X which follows the chi-square distribution if its pdf is of the form

F(x)= 1/(n/2).e^-x/2.x(^n/2)-1,                 0<x<∞

 

The variable n is a positive integer, and that is called the number of degrees of freedom.

A variable that will follow the chi-square distribution correctly will be called as a chi-square variate.


Properties:

1. The chi-square curve has to be positively skew.
2. Mean = n, σ² = 2n, (n = d.f.)

• If x2 is a chi-square variate with ndf., then x²/2 is a Gamma variate with parameter (n/2).

1. If X_i (i = 1, 2, … , n) are n independent normal variates with mean  µ_i; and variance σ²_i (i = 1,2, … ,n) then x2=Σ_i (X_i-µ_i/σ_i)is a chi-square variate with ndf
2. M.G.F. = (1 – 2t)^-n/2,            |2t| < 1
3. In practice, for n ≥ 30, the x² distribution is estimated by normal distribution.

 

(j) Student’s t-distribution. A random variable iffollows the student’s t-distribution or just -distribution if its pdf is given by

f(t) = y₀ (1+ t2/n)^-(n+1)/2      ,- ∞ < t <∞

Where, y₀ is a constant variable so that the area under the curve is unity and n are called degrees of freedom.

Properties:

• The t-curve is symmetrical about 0, and leptokurtic i.e., β1 = 0,
• Mean = 0, Variance =n/(n-2),           (n > 2)
• For large df, the t-distribution can be approximated by the standard normal distribution.
• Let X_i (i = 1,2, …, n) be the random samples from a normal population having mean µ and variance σ₂, then the statistic

 

 

(k) F-distribution; A random variable is said to be F-distribution with degrees of freedom (v1, v2) if its pdf is of the form

f (F) = y₀F^(n/2)-l ( V₂ + v1 F)^-(v1+v2/2)

Where, y₀ is a constant such that the area under the curve is unity

n is the degrees of freedom.

 

Properties: 

(i) The F-curve is positively skew.

(ii) Mean = v2/ (v2 – 2)

Variance = 2(v₁ + v₂ – 2)/v₁(v₂-4). (v₂/v₂-2)²

(iii) If y1 and y2 are independent chi-square variates with n1 and n2 degrees of freedom, then we are left with= y1/n1/ y2/n2, follows F-distribution with (n1, n2) df.

Links of Previous Main Topic:-

• Introduction to statistics
• Knowledge of central tendency or location
• Definition of dispersion
• Moments
• Bivariate distribution
• Theorem of total probability addition theorem
• Random variable
• Binomial distribution

Links of Next Statistics Topics:-

• What is sampling
• Estimation
• Statistical hypothesis and related terms
• Analysis of variance introduction
• Definition of stochastic process
• Introduction operations research
• Introduction and mathematical formulation in transportation problems
• Introduction and mathematical formulation
• Queuing theory introduction
• Inventory control introduction
• Simulation introduction
• Time calculations in network
• Introduction of game theory