Defining the theorem:
The reversible heat engine is known to be the most perfect and efficient one working in two fixed temperatures. It is believed that there are no other heat engines with such proper workability.
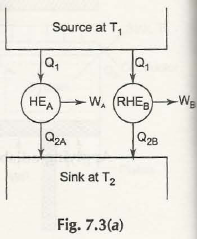
Consider the figure below:
Let HEA = Any heat engine
RHEB= Reversible heat engine and both the engine draw Q1 amount a heat.
Suppose the statement is not true, so,
Either we come to, WA / QA> WB / Q1
Or, WA> WB
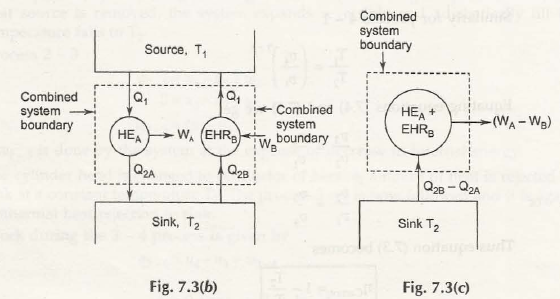
Now we reverse the RHE8 as it is reversible, so all directions of flow will be reversed.
For this matter you should consider the figure below,
If we combine HEA& EHRB, we get work W A – W 8 out of exchange heat (Q2B – Q2A) with single temperature sink T2. Thus it violates Kelvin-Planks law, so ɳ B>ɳ A is true which means that HEA is also a reversible heat engine.
This is when you’ll require knowledge over Corollary of Carnot’s theorem.
Defining Corollary of Carnot’s Theorem:
Any type of reversible engines that will perform in the two same and fixed temperatures will have equal workability. For proving this theorem we will consider the equation below:
We already have, ɳ B>ɳ A for B reversed
ɳ A>ɳ B for A reversed
ɳ A>ɳ B proved for both the engines are reversible.
Links of Previous Main Topic:-
- Statement of zeroth law of thermodynamics with explanation
- Heat and work introduction
- Open system and control volume
- Conversion of work into heat
- Introduction to carnot cycle
- Efficiency of carnot cycle
- Carnots theorem
Links of Next Mechanical Engineering Topics:-
- Absolute thermodynamic temperature scale or kelvin scale
- Absolute zero on thermodynamic temperature scale
- Clausius inequality entropy and irreversibility introduction
- Ideal gas or perfect gas
- Introduction about air standard cycles
- Properties of pure substances introduction
- Vapour compression refrigeration cycle introduction
- Basic fluid mechanics and properties of fluids introduction