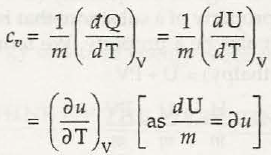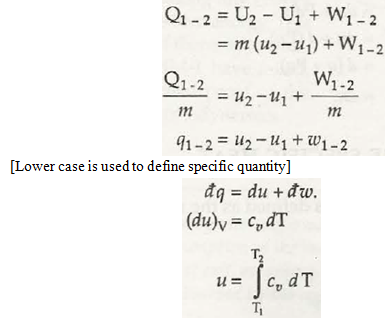In case of an ideal gas which is found at constant pressure would surely take up more heat in order to gain same level of temperature change and that too at constant volume. When there is constant volume heats get added up and finally help to increase temperature. At constant pressure there is some heat that would perform work.
Q = nCPΔT
For ideal gas, it is important to apply First Law of Thermodynamics which would say that the heat is equal to:
Q = ΔEint + W
When there is constant pressure then, W = P∆V = nR∆T
But, in case of monatomic gas, it is said ΔEint = (3/2)nRΔT, we get:
Q = (3/2)nRΔT + nRΔT = (5/2)nRΔT
So, for a monatomic ideal gas:
CP = (5/2)R
For diatomic and polyatomic ideal gases we get:
Di-atomic: CP = (7/2)R
Polyatomic: CP = 4R
Links of Previous Main Topic:-
- Statically indeterminate system
- Introduction to thermodynamics
- Statement of zeroth law of thermodynamics with explanation
- Heat and work introduction
- First law of thermodynamics for a control mass closed system undergoing a cycle
- First law of thermodynamics for a change of state for a control mass closed system
- Different types of stored energy
- The constant volume specific heat
Links of Next Mechanical Engineering Topics:-