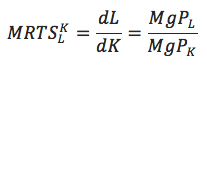In this appendix represents a Mathematical treatment with the help of cost theory and basics of production. Till appendix to Chapter 04, we are using the method of Lagrange multipliers for solving the problems of firm cost minimising.
Concept of Cost minimization
Cost minimization is a kind of tool used in the field of pharmaeconomics as to make comparison of the cost per course treatment. The theory of the firm based on the assumption which firm choose to get input into production process that helps in minimising the cost of producing the output. For instance there are two inputs, Capital K, Labor L, the production function F (K, L) depicts maximum output which can be produced or making the every possible combination of inputs. The result of production in all these process is positive but lead to decrease in the marginal product. The marginal
Product of Labor and capital will be presented MPL (K,L) and MPL(K,L).
When any firm take prices of Labor and capital as w and r respectively, the value of cost-minimization problem will be-
C = wL + Rk
If the subject to constraint is able to produce fixed output as q0, then-
F (K, L) = q0
C represents cost of producing fixed level of output q0.
How to make determination of firms demand for Labor and Capital input
Firms make choice of demand by making use of different kind of inputs. The most common form is capital and Labor. The determination of demand and supply take place in the labour market. The main participants of Labor market are workers. Worker do supply of labors to the firms in exchange of the wages. Firm also made a demand of labors in exchange of the wages.
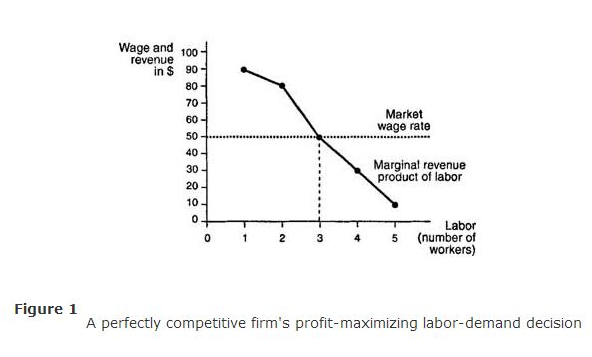
Demand of firm for Labor: The firm demand of labour is a form of derived demand. It is derivation of firm’s output. If the demand of firm for output will increases then directly demand for Labor also. If the demand of firm decreases then directly demand for workforce also reduced to some extent.
Concept of Marginal revenue of product for Labor: When the firm is well aware of demand for output, it can easily determine that how much should be Labor need for getting right marginal revenue of the product. Marginal revenuer of a product is an additional form of revenue which a firm usually earns by employing unit of Labor.
The firm’s Labor demand curve. The firm’s profit‐maximizing Labor‐demand decision is depicted graphically in Figure.
- All the economic decisions are result of problem of optimization which is subject to the series of constraints.
- Consumer makes the decision regarding what to buy keeping in mind fact that your choice should be affordable
- Firms make the decision to maximise the profits subject to constraints with an aim of having limited production capacity.
- Households make decisions that how much have to do work playing with your constraints as per the hours of the day.
- Firms do minimisation of cost subject to constraints the orders they have to fulfil.
All these issues fall under categories of constrained optimization. In a uniform process one needs to solve the issues.
Marginal rate of technical substitution
MRTS or Marginal Rate of Technical Substitution is defined as keeping the value of total output remains constant, it is calculation of how much to decrease one input to increase other input. It is like showing of relation between the inputs and various trade-offs among them without making any changes in level of output. We can see that combinations get changed as per the value of isoquant changes. It can be written by total derivative of F(K, L). its value will be equal to zero ordq= 0. The MRTS can also be written as-
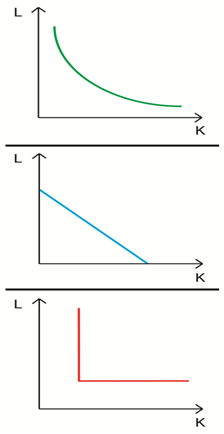
The marginal rate of technical substitution is equivalent to the slope of isoquants. Below mentioned figures one understands about the forms of isoquants.
In the first diagram of Marginal rate of technical substitution change along with the curve will be at zero level when it diminishes quantity of L along with the infinity when diminishing quantity or value of K.
When we look at second diagram, both its inputs are exact substitutes, since these lines are parallel to each other where MRTS is equal to one. Its slope has 45 degree angle with each axis. When we are considering the substitutes of inputs, as a result slope will become different and MRTS is defined as fraction that might be 1/2, 1/3, etc. For perfect substitutes, the value of MRTS remains constant.
In third graph, it represents complementary inputs. The value of horizontal fragment of each isoquant for theMRTS will be equal to zero (0) and vertical fractions for the MRTS will be equal to infinity(∞).
Duality in Production and Cost Theory
If we consider the input decision of firm, it is actually dual in nature. We have to find optimum inputs to get a question of choosing the lowest line for is cost. The tangent of isoquant production will show the choice of higher production. In other words, we can say that isoquants are the other functions of input allocation. The solution of these inputs come when the result shows highest input value.
The Cobb-Douglas Cost and Production Functions
In Economics, the term Cobb-Douglas Cost and Production Function is a kind of production function that use widely to make a representation of a technological relationship between the amounts of two or more than two inputs particularly physical capital and Labor. The amount of output produces with those inputs. Mostly used in forecast production and macroeconomics.
The Cobb-Douglas production function
- Here Q is the quantity which produces from the input L and K
- L is the amount of Labor expended that is expressed in hours.
- K represents the amount of physical capital input which includes operation, factory or machine.
It helps in projecting risk analysis especially in construction projects and also related to the construction schedule crashing. Con-Douglas production defined portion of equipment and labor needed on the basis of production rates. This is a new form of perspective that fill all gaps between existing time-cost trade-offs research by doing proper consideration of project duration equipment cost and labor.
Links of Previous Main Topic:-
- Introduction Markets and Prices Preliminaries
- The Basics of Supply And Demand
- Consumer Behavior
- Appendix to Chapter 4 Demand Theory a Mathematical Treatment
- Uncertainty and Consumer Behavior
- Production
- The Cost of Production
Links of Next Microeconomics Topics:-