The appendix depicts basics of the demand theory through mathematical treatment.The target readers are students who are familiar with calculus and its application. The aim is to give a short brief of the theory of demand to such students. To attain this goal, we will use the concept of constraint optimization.
Consumer behavior theory is based on hypothesis that consumers intend to maximize the utility subject to constraint of a limited budget. As was depicted in Chapter 3, a utility function can be defined for every consumer. The utility function attaches to each market, a level of utility. We also defined marginal utility of goods as change in a utility linked with one-unit rise in the good’s consumption. With the use of calculus, we will measure the marginal utility as utility change which results from a small rise in the consumption.
For instance, let there be a utility function represented by the equation provided below. U(X, Y) = log X + log Y
Let X represent food and Y represent clothes. The marginal utility linked to the additional food consumption can be expressed in the form of partial derivative of utility function with respect to food X. Marginal utility of food will be represented as follows-
MUX = ∂U(X, Y)/∂X = ∂(log X + log Y)/∂X = 1/X
The marginal utility is considered to decrease with consumption and utility level is an increasing function of the goods consumed. If we have two goods, X and Y, optimization problem can be given by the below expression-
Maximize U(X, Y) (A4.1)
Considering that entire income is spent on two goods-
Px X + Py Y = I (A4.2)
I – Income
X –Quantity of Good 1
Y – Quantity of second good
U() – Utility function
Px and Py are commodity prices
To calculate consumer’s demand for both goods, we opt for values of X and Y so as to maximize (A4.1) subject to (A4.2). Once we know utility function’s particular form, consumer’s demand can be calculated directly for X and Y. In its general form the utility function is defined as U(X,Y). Constrained optimization can be employed to figure out the conditions that need to be met in order to maximize the utility.
The Method of Lagrange Multipliers
This method can be employed as a technique to minimize or maximize a given function under a certain set of constraints.A detailed application of this technique is used to find consumer’s optimization provided by equation A4.1 and equation A4.2. We will also employ this technique later to analyze cost and production issues.
- A statement of the Problem- First of all, we need the Lagrangian for the given problem. The function to be minimized or maximized is called the Lagrangian. In this case, the Lagrangian is the utility being maximized. The consumer’s budget is the constraint.
The Lagrangian will be expressed as-
ᵩ = U(X, Y) – ƶ(PxX + PyY – I) (A4.3)
We have specified budget constraint as-
PxX + PyY – I = 0
The summation is equal to zero. Now, we can use this summation in the Lagrangian.
- Differentiating Lagrangian- The second term in the equation A4.3 is equivalent to zero if the values of X and Y are chosen to satisfy the budget constraint. The function is maximum when U(X, Y) is maximum. Let us differentiate ᵩ with respect to X, Y and ƶ. The derivative is then equated with zero to achieve the condition of maxima. The equations provided below specify the same.
∂ᵩ/∂X = MUx(X, Y) – ƶPx = 0
∂ᵩ/∂Y = MUy(X, Y) – ƶPy = 0 (A4.4)
∂ᵩ/∂ƶ = I – PxX – PyY = 0
MU signifies marginal utility.
MUx(X, Y) = ∂U(X, Y)/∂X
It is the change in utility caused due to small rise in consumption of good X.
- Solving the Equations The above mentioned equations A4.4 can be rewritten as follows-
MUx= ƶPx
MUy= ƶPy
PxX + PyY = I
On solving these three equations, we obtain the values of X and Y. These values are the utility maximizing values for the optimizing problem.
The Equal Marginal Principle
Equation no. 3 PxX + PyY = I is the budget constraint of the consumer.
Equations number 1 and 2 show that the goods X and Y get consumed to a point where marginal utility is multiple (ƶ) of price of the goods.
On combining the first two conditions, we get the equal marginal principle.
Ƶ = MUx(X, Y) / Px = MUy(X, Y) / Py (A4.5)
This shows that marginal utility of both goods divided by the price is same.
In order to achieve the optimal condition, consumer should get same utility from last dollar used by consuming X or Y. If this isn’t the case, consuming one item more than the other or one item less than the other will raise the utility.
Information provided in A4.5 can be written in below form to analyze the optimization in greater detail.
MUx(X, Y) /MUy(X, Y)=Px/Py (A4.6)
Thus, ratio of marginal utilities is equal to ratio of commodity prices.
Marginal Rate of Substitution
Chapter 3 explained the relation between indifference curves and utility functions. Equation A4.6 can be used to see this link.
All the market baskets that provide the consumer same level of the utility are represented by indifference curve. Let U* be a fixed utility level, indifference curve corresponding to utility level is signified by below relation-
U(X, Y) = U*
Any alterations made to the items X and Y will affect the market baskets. On increasing X by a small amount and decreasing Y by a small amount, the overall change in the utility must come out to be zero. This is signified by below equation-
MUx(X, Y)∂X + MUy(X, Y)∂Y = ∂U* = 0 (A4.7)
The above equation can also be written as follows-
-∂Y/∂X = MUx(X, Y)/MUy(X, Y) = MRSxy (A4.8)
MRSxy- this is marginal rate of substitution of X for Y. The left-hand side of the equation A4.8 depicts in difference slope’s negative curve. At tangency point, the marginal rate of substitution is equivalent to the ratio of marginal utilities. The ratio of marginal utilities is equivalent to ratio of prices of X and Y, i.e. the two goods, as shown in A4.6. When individual indifference curves are convex in shape, tang ency of this indifference curve to budget line provides solution to the optimization problem. This was shown in Chapter 3 in Figure 3.13 (on page 86).
Marginal Utility of Income
Irrespective of what the form of utility function is, Lagrange multiplier ƶsignifies the added utility which is generated when budget constraint is eased/relaxed. In order to depict how the principle works, the utility function U(X, Y) is differentiated with respect to I.
∂U/∂I = MUx(X, Y)(∂X/∂I) + MUy(X, Y)(∂Y/∂I) (A4.9)
The increase in income I must be divided between both items X and Y.
∂I = Px∂X + Py∂Y (A4.10)
Let us substitute values from equation A4.5 into equation A4.9.
∂U/∂I = lPx(∂X/∂I) + lPy(∂Y/∂I) = l(Px∂X + Py∂Y)/∂I (A4.11)
On substituting equation A4.10 into equation A4.11, below equation is obtained-
∂U/∂I = l(Px∂X + Py∂Y)/(Px∂X + Py∂Y) = l (A4.12)
Hence, Lagrange multiplier is an extra utility resulting from relaxation in the budget.As per the original analysis to determine the condition of utility maximization, equation A4.5 shows that utility maximization requires utility obtained from consumption of each and every good to be equal to marginal utility of the extra dollar of income. If the case were any different, the utility could be raised by spending more on good with greater ratio of the marginal utility to item price and less on other good.
An Example
The equations in A4.4 can be solved to find out the unknown variables X, Y, and ƶas function of two prices and the income. Substituting for ƶ allows us to solve for demand of both the goods in terms of commodity price and income. Let us understand this with the help of an example.
Cobb-Douglas is a frequently used utility function.The function can be depicted in below two ways:
U(X, Y) = a log(X) + (1 – a) log(Y) and U(X, Y) = Xa Y1-a
Both forms are identical to each other and give identical demand functions for the goods X and Y. Let us use the first form to derive demand function.
Let us write the Lagrangian for this purpose-
ᵩ =a log(X) + (1 – a)log(Y) – ƶ(PxX + PyY – I)
Let us differentiate the above equation with respect to X, Y and ƶ.
∂ᵩ/∂X= a/X – ƶPx= 0
∂ᵩ/∂Y= (1 – a)/Y – ƶPy= 0
∂ᵩ/∂ƶ = PxX + PyY – I = 0
From the first two relations-
PxX = a/ƶ (A4.13)
PyY = (1 – a)/ƶ (A4.14)
Let us combine equations A4.13 and A4.14 with condition of budget constraint.
a/ƶ + (1 – a)/ƶ – I = 0
- Ƶ = 1/
Let us replace the value of ƶ into A4.13 and A4.14 to get demand function.
X = (a/Px)I
Y = [(1 – a)/Py]I
The cross price elasticity is considered zero in the example. This means the demand of a good depends on its price and income. It is independent of price of other good. Lagrange multiples can be understood through this example.We can replace the values in the equation with specific values.
Let us consider-
a to be 0.5
Px = $1
Py = $2
I = $100
The utility is maximum when values of X and Y are 50 and 25 respectively and ƶ = 1/100. As per Lagrange multiplier if one extra dollar of income is available, the utility level would rise by 1/100. Let us check this in detail. If the income increases by a dollar, the total income stands at $101.The values of X and Y for maximization are 50.5 and 25.25 respectively. The original utility level was 3.565 and the new utility level is 3.575. The extra dollar has thus raised the utility by 1/100 i.e. 0.01.
Duality in Consumer Theory
Consumer’s optimization decision can be looked upon in two separate ways. The optimum values of the commodities X and Y can be analyzed as the values for which the value of U() is maximum and the indifference curve is the highest. Another way to look at the values is from the perspective of choosing lowest budget line and the lowest budget expenditure. This two-way perspective is referred to as duality.
Let us understand this with the below dual consumer optimization problem.
The aim is to minimize the cost of a particular utility level subject to a constraint.
Minimize PxX + PyY with constaint that U(X, Y) = U*
The Lagrangian for this entity is-
ᵩ = PxX + PyY – µ(U(X, Y) – U*) (A4.15)
Here μ is Lagrange multiplier.
Let us differentiate ᵩ with respect to µ, Y and X and equate the derivative with zero to find the condition for minimum expenditure.
Px- µMUx(X, Y) = 0
Py- µMUy(X, Y) = 0
U(X, Y) = U*
Let us solve these two equations and recall equation A4.5
µ = [Px/MUx(X, Y)] = [Py/MUy(X, Y)] = 1/ᵩ
Also, MUx(X, Y)/MUy(X, Y) = MRSxy= Px/Py
The optimal values of the commodities X and Y are found at point of tangency of budget line and indifference curve which generates the utility U*. As we can see, these points are the same points that maximized the utility in original problem. Dual expenditure minimization problem gives same demand functions that are obtained from direct utility-maximization problem.
For analyses purpose of dual approach, let us take the Cobb-Douglas example once again. The exponential form of the utility function is given by U(X, Y) =Xa Y1-a
The Lagrangian for this will be given by-
ᵩ = PxX + PyY – µ[X^a Y^(1-a)- U*] (A4.16)
Let us differentiate equation with respect to X, Y and µ and equate the derivative with zero.
Px= µaU*/X
Py= µ(1 – a)U*/Y
Let’s multiply first equation by X and second equation by Y and add the two equations-
PxX + PyY = µU*
Let I be the cost-minimizing expenditure (if entire income was not spent to get utility level U*, U* would not have maximized utility in original problem). So μ = I/U*. If we substitute this value in the above equations for the values of X and Y, we get-
X = aI/Px and Y = (1 – a)I/Py
As is clear from this illustration, the same demand function is obtained as before.
Income and Substitution Effects
Demand functions set up a relationship between utility maximizing choices and their response to change in income and group prices. We need to distinguish the portion of any price change that involves movement along an indifference curve from that portion which involves movement to a different indifference curve (and hence change in the purchasing power). In order to make this distinction, let us consider the change in demand of good X and its price changes. The change in the demand can be divided into a substitution effect (change in demand of quantity when level of utility is fixed) and an income effect (the change in demand of quantity with level of utility changed but with relative price of good X unchanged).
The change in X caused due to a unit change in price of X, holding utility constant is denoted as-
∂X/∂Px|u = u*
Total change in quantity demanded of X resulting from a unit change in Px is-
∂X/∂Px= ∂X/∂Px|u=U* + (∂X/∂I)(∂I/∂Px) (A4.17)
First term on right in equation depicts substitution effect since utility is fixed and second term is income effect since income increases.
From the budget constraint, I = PxX + PyY, from differentiation we have-
∂I/∂Px= X (A4.18)
If the consumer owns goods X and Y, equation A4.18 shows that when price of good X is increased by $1, income obtained from good sale increases by $X.
However, in accordance with the consumer behavior theory, the goods are not owned by the customer. Thus, equation A4.18shows the additional income consumer would require in order to nullify the price change.
So we will write the income effect as negative (courtesy of lack of power to purchase). Equation
A4.17 becomes-
∂X/∂Px= ∂X/∂Px|u=U* – X(∂X/∂I) (A4.19)
Equation A4.19 is called Slutsky equation.
The first term is the substitution effect and second term is the income effect.
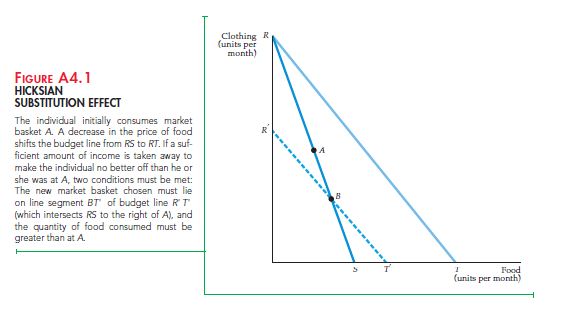
There is another method to split the equation into substitution and income effects which doesn’t need indifference curves. This approach was bought forth by John Hicks and is called Hicksian substitution effect.
As shown Figure A4.1, first of all the consumer needs to choose market basket A on the budget line RS. Now, if the price of commodity (food) falls and budget line moves to RT, we take away a portion of the income to bring the consumer to the same position as before. To achieve this, we draw a budget line parallel to RT.
If the budget line passed through point A, the consumer will be in at least the same position as before. He can still opt to purchase market base A.
As per the Hicksian Substitution effect, a budget line (like R’T’) that is parallel to RT and intersects RS at a point B which is below the point A and to the right of A, leaves the consumer equally well off.
Links of Previous Main Topic:-
Links of Next Microeconomics Topics:-
- Appendix to Chapter 4 Demand Theory a Mathematical Treatment
- Uncertainty and Consumer Behavior
- Production
- The Cost of Production
- Production and Cost Theory A Mathematical Treatment
- Cost in the Long Run
- The Cost of Production Production with Two Outputs
- Profit Maximization and Competitive Supply
- The Analysis of Competitive Markets
- Market Power Monopoly and Monopsony
- Monopolistic Competition and Oligopoly
- Game Theory and Competitive Strategy