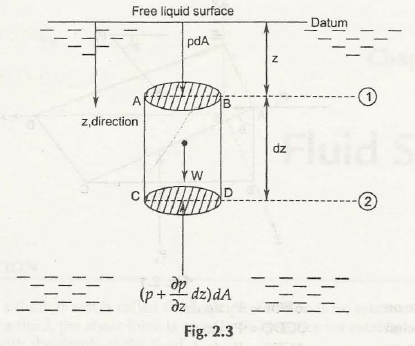
Consider a cylinder is at rest. The fluid element of cylinder with the action of forces is shown in Fig.2.3
Let pdA be the force on section AB at a distance z from the datum.
dz be the height of cylinder
(p + ∂p/∂zdz)dA be the force on section CD whose distance from datum is (z + dz)
W be the weight of cylinder
Then,
Forces can be written as (in z-direction),
∑▒Fz = 0
pdA + W – (p + ∂p/∂zdz)dA = 0
or,
∂p/∂zdzdA = W
Or,
w = ∂p/∂z
ρ . g = dp/dz (ρ = Mass Density)
This suggests that rate of depth dp/dzis equal to the weight density of fluid.
The above equation can also written as-
p2 – p1= ρ. g (z2 – z1)
or,
p = . g .z
Links of Previous Main Topic:-
- Introduction about air standard cycles
- Properties of pure substances introduction
- Vapour compression refrigeration cycle introduction
- Basic fluid mechanics and properties of fluids introduction
- Fluid statics introduction
- Fluid pressure at a point
- Pascals law
- Pressure density height relationship
Links of Next Mechanical Engineering Topics:-