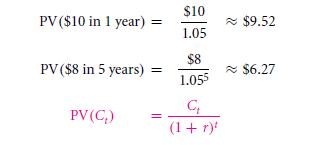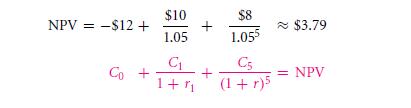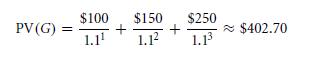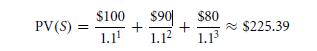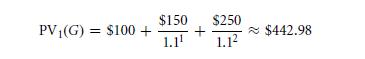Net Present Value

The cash flows are translated to cash in the same unit – this is the most crucial advantage of the present value. The project that will generate a value of $10 in a year & $ 8 in the 5 years duration is beneficial. You hence cannot sum up all these to the future values and come with the value of $18 – then it becomes the situation of adding up oranges with apples. Yes, it is that vague. However, when you translate the future cash flows with the certain present values, then you can add these two up. Let us give an example, in case the interest rate was taken to be 5% in a year, so, it will be (1 + 5%)⁵ = (1 + 27.6%) that being for over the period of five years. Then present value will be,

Thus, the worth of the work’s future cash flow will be at the present time period and the value will be $15.79.

NPV or net present value of an investment will be that of a present value that is of all the future present cash flows subtracted from the many present value of the cost. Thus it is mostly similar to the present such value with that of the except for the term ‘net’, which reminds you gently to add & minus all the possible cash flows. This is done in inclusion to an up front investment that is being given today. The calculation that is needed for this particular method is,

• Translating the various future cash flow to present dollars
• Adding these up giving all such present value which are future cash flow
• Subtracting the investment that is made initially

NPV is a very important method that is used to determine the certain value of all such project. Thus it is in fact best called as the keystone of finance. Assuming there are many uses you have to be able topay for $12 in order to make a purchase of this project with a $10 and that of $8 cash flow respectively, the NPV will be a positive one. This is as,

(Keeping in mind of your convenience, we have omitted the zero from the subscript which is for NPV, as that we did that for PV.)

There are many ways of understanding the net present value.

• The one way to think and consider the total NPV is that of $3.79 is to calculate the difference in both existing value of cash flows in the market with the project cost – this is termed as the difference in the ‘value added’.
• The other way to consider is by thinking that the project is hence to compare the cash flows of it to the sets of all the bonds which are replicates of them. In an instance, no one would ever want to make a purchase in a one year bond with promises of $10 on the consecutive year. As you will save $9.52 – this will be of a return interest rate of 5% – as you can get a $10. Similar to this a five year bond which will promise a $8 in a year for five years, will yield $6.27. Altogether with the two bonds, you can replicate projects cash flows. This is when law of one price will say that the project must be worth equal to the value of the bond. This is as there is that of cash flows which are identical to one another. You would get a cash flows of $12 only as a much better option as the bond is alternative.
• There is another certain way to consider of the NPV. That is when you compare two projects to the main alternative opportunity issues of investments in a capital market. The opportunities are mostly expressed as a denominator by discount factor is. Then what would the $12 investment look like if you are to invest them in capital markets? Using the future value formulas, that you can earn the value with 27.6% from 5 years. All that your money will grow up to is $12.60 right to the upcoming future year. You can also take the absolute same amount of $10 cash flow and will be done with $2.60. This money can be further reinvested. On the upcoming four years, this is a mere 5% interest rate, which will make your $2.60 to $3.16. As the project grows better, it grows into $8. Hence, the project that you achieve is having a complete high rate of returns compared to the common capital markets.

Hence, it is concluded as the argument is simple and best capital budgeting rule is that: NPV if, is positive, then, you must take on a project. If the value comes up as negative, you must immediately reject a fellow project. It the value comes to zero, and then it will not matter.

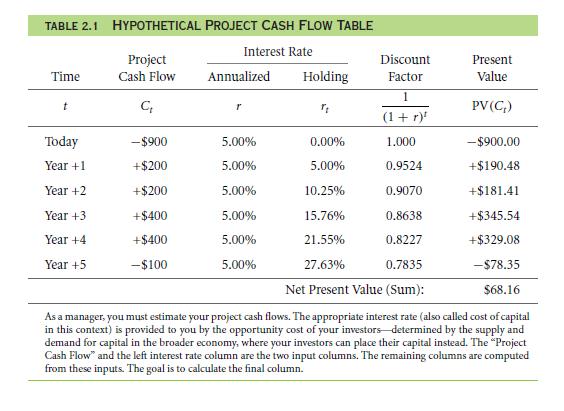
Let us see another work that NPV has given. A project will cost $900 and yielding $200 a year for the last two years, where then the $400 every year for two years will it clean the value expenditure of $100.

This interest rate that is accounted is 5% every year. When the cash flows are categorically summarized, that you can witness on table 2.1, would you take on the project?

1. The thing that one needs to determine is that cost of capital that is involved for one year, two years, and thus on. Compounding formula will be,

(1 + r_t) = (1 + r)^t = (1.05)^t = 1.05^t

Hence, for the money that is invested at this point, the cost of capital r₀will be 1.050 − 1 = 0; for money value in one year r₁ is 1.05¹ − 1 = 5%; for money value in 2years, and r₂ is 1.05² − 1 = 10.25%. So you get the idea.

1. You will need a translation to manage this cost of capital. The dollar that was 1 year in worth will be 1/(1 +5%) = 1/1.05 ≈ 0.9524 dollar on the present date. The dollar will be that of two years is worth 1/(1 + 5%)2 =1/1.052 ≈ 0.9070. This will continue.

• Now, you can easily translate the cash flows that is obtained in the future with the present value of equivalents that is by multiplying all the payoff values with appropriate total discount factors. Like in the example, $200 of a cash flow at a time of 1 year, will be worth around, 0.9524 . $200 ≈ $190.48.

1. This is because the present values that are all additional and thus, you can add them up to all the various terms will add up to a total of the net present value. It is necessary to make sure that all the upfront cost is taken as negative.

The project of NPV is that of $68.16. This is because the positive value must be taken in the project

Though, the upfront such expense will have to be $1000 in place of the $900. The total NPV should have been (−$31.84) which is negative if you invested the money somewhere else rather than the bond. Is such a case, rejecting the project is the right decision.

2.6A Application: are faster-growing firms better bargains?

The NPV problem is a massive one. As it applies to the entire company. So, will it make a difference, if the companies are to invest to grow faster than the slow rate? Think this question, though, just not slowly. On whether one should purchase stocks form fast expanding companies like that of Google? Rather or should you wait with a slowly growing brand like Procter and gamble? The ideal answer should be as this is a choice that it will not matter on the perfect market. The growing rate of a firm is insignificant. As, the present market value suggests, the firms cash flows will always accrue to their owners.

This is why none of the two deals are better than the other.

Let us consider, the company, ‘grow’ (G), which will be producing over the coming 3 years,

G1= $100

G2= $150

G3= $250

This and the company’s ‘shrink’ (S) will be producing

S1= $100

S2= $90

S3= $80

Then, is G not a much better brand than S?

No uncertainty will be involved, as both the brands will face equal and equivalent cost of capital which is 10% on a yearly basis.

So, for G,

And now, the price range of S,

Thus, if you are investing in G and the next year will give a cash of $100. G’s value will be over one year,

The investment that you make will earn you a rates of return, $442.98/$402.70 − 1 ≈ 10%.

If you have chosen the company S to invest in, it will yield after a year,

The investment that you make will be earned at this rate of return that is, $247.93/$225.39 − 1 ≈ 10%. Thus in both cases, you earn a fair share of rate of return which is 10%. Be the cash flows growing rate any; it is irrelevant, like +50%, −10%, +237.5%, or −92%. The market price of a firm is a reflection of its future growth rate. There will be no certain connection pattern among growth rates which are so much of dormant project of cash flows / equity earning. This is the product of invested money.

The statement that is presented before you says that the higher amounting growth of the brands earn higher rates of return. This does not definitely mean that the investments made on a lower growth rate company is less, these firms just produce in a slower but steady rate.

Summary

Key terms

Solve now! Solutions

Problems

Links of Previous Main Topic:-

• Introduction of corporate finance
• The time value of money and net present value

Links of Next Financial Accounting Topics:-

• Stock and bond valuation annuities and perpetuities
• A first encounter with capital budgeting rules
• Working with time varying rates of return
• Uncertainty default and risk
• Risk and return risk aversion in a perfect market
• Investor choice risk and reward
• The capital asset pricing model
• Market imperfections
• Perfect and efficient markets and classical and behavioral finance
• Capital budgeting applications and pitfalls
• From financial statements to economic cash flows
• Valuation comparables financial ratios
• Corporate claims
• Capital structure and capital budgeting in a perfect market
• The weighted cost of capital and adjusted present value in an imperfect market with taxes
• What matters
• Equity payouts
• For value financial structure and corporate strategy analysis
• Capital structure dynamics firm scale
• Capital structure patterns in the united states
• Investment banking and mergers and acquisitions
• Corporate governance
• International finance
• Options and risk management