To derive the continuity equation in three dimensions in differential form, we consider the concept of control volume as shown in Fig. 4.5
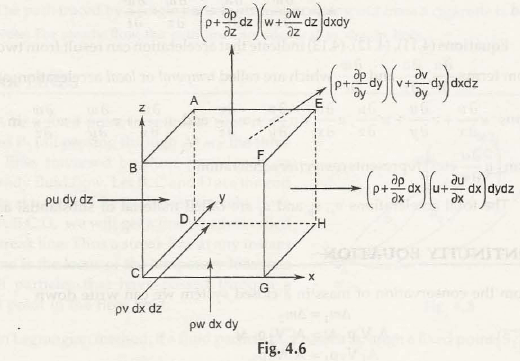
Take an element of fluid from the control volume and control surface to create rectangular parallelepiped as shown in Fig. 4.6
Let us consider mass is entering from ABCD surface and leave the body from EFGH in xdirection.
Rate of mass enters the fluid element = ρudydz
Rate of mass leaves the fluid element = (ρ + ∂ρ/∂x dx )(u + ∂u/∂x dx )dydz
= [ρ u + ρ ∂u/∂x dx + u ∂ρ/∂x dx + ∂ρ/∂x. ∂u/∂x 〖(dx)〗^2 ]dydz
= [ρ u +(∂(ρu))/∂x dx] dydz {∂ρ/∂x. ∂u/∂x 〖(dx)〗^2 is neglected}
We know that,
For control volume:
Rate of mass entering control volume = Rate of mass leaves + Rate of accumulation of mass
Substituting the values, we get-
ρu dydz = [ρ u +(∂(ρu))/∂x dx]dydz + Rate of accumulation of mass
Thus,
Rate of accumulation of mass = ρu dydz – [ρ u +(∂(ρu))/∂x dx]dydz
= – (∂(ρu))/∂xdxdydz
Similarly,
Rate of accumulation of mass in y direction can be given by,
= – (∂(ρv))/∂ydxdydz
And,
Rate of accumulation of mass in z direction can be given by,
= – (∂(ρw))/∂zdxdydz
Adding all above equations of rate of accumulation of mass, we get the rate of accumulation of the element rectangular parallelepiped-
= –[(∂(ρu))/∂x + (∂(ρv))/∂y + (∂(ρw))/∂z]dxdydz
Or,
∂ρ/∂tdxdydz = –[(∂(ρu))/∂x + (∂(ρv))/∂y + (∂(ρw))/∂z]dxdydz
Or,
∂ρ/∂t= –[(∂(ρu))/∂x + (∂(ρv))/∂y + (∂(ρw))/∂z]
Or,
∂ρ/∂t + [(∂(ρu))/∂x + (∂(ρv))/∂y + (∂(ρw))/∂z] = 0 (General Continuity Equation)
Note:
The above general continuity equation is applicable to:
Uniform Flow and Non-uniform Flow
Steady Flow and Unsteady Flow:
For steady flow, ∂ρ/∂t= 0
Then, continuity equation becomes
(∂(ρu))/∂x + (∂(ρv))/∂y + (∂(ρw))/∂z= 0
Compressible Flow and Incompressible Flow
For incompressible flow, ∂ρ/∂t= 0 andρ = constant
Then, continuity equation becomes
∂u/∂x + ∂v/∂y + ∂w/∂z= 0
If we consider the above equation in vector form, then it can be written as-
∂ρ/∂t + V ⃗. (ρV ⃗) = 0
Where,
V ⃗ = Velocity Vector = i ̂ ∂/∂x +j ̂ ∂/∂y +k ̂ ∂/∂z
Suppose the density ρ of liquid remains same with time that means ∂ρ/∂t= 0
Hence,
V ⃗. (ρV ⃗) = 0
If the density ρ = constant, then the above equation can be written as-
V ⃗. (V ⃗) = 0
Links of Previous Main Topic:-
- Vapour compression refrigeration cycle introduction
- Basic fluid mechanics and properties of fluids introduction
- Fluid statics introduction
- Manometers measurement pressure
- Fluid kinematics
- Lagrangian method for describing fluid method
- Eulerian method for describing fluid method
- Lagrangian relationship from eulerian equations
- Steady and unsteady flows
- Uniform and non uniform flows
- Stream line
- Path lines
- Streak lines
- Acceleration of a fluid particle
- Continuity equation
- Continuity equation in three dimensions in differential form
Links of Next Mechanical Engineering Topics:-