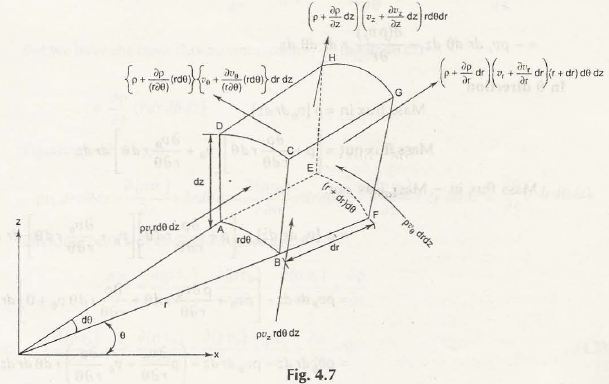
We have already derived the continuity equation in three dimensions in differential form. It is also possible to get continuity equation using the same system for all flows in a cylindrical polar coordinate system as shown in Fig. 4.7
Suppose the coordinate system of an elementary control volume be (r, θ, z)
In the direction of r, the Rate of mass enters the system can be given by ρvr rdθdz
Rate of mass leaves the system be (ρ + ∂ρ/∂r dr)(v_r + (∂v_r)/∂r dr) rdθdz
Since,
For control volume:
Rate of mass entering control volume = Rate of mass leaves + Rate of accumulation of mass
Substituting the values, we get-
ρvrrdθdz = (ρ + ∂ρ/∂r dr )(v_r + (∂v_r)/∂r dr )rdθdz + Rate of accumulation of mass
Or,
Rate of accumulation
of mass = ρ [vrrdθdz] – (ρ + ∂ρ/∂r dr )(v_r + (∂v_r)/∂r dr )rdθdz
= ρ [vrrdθdz] – [ρvr + ρ (∂v_r)/∂r dr + vr∂ρ/∂r dr + ∂ρ/∂r . (∂v_r)/∂r(dr)2] [rdθdz + drdθdz]
Neglecting higher order terms, so ∂ρ/∂r . (∂v_r)/∂r(dr)2 = 0
Or,
= ρ [vr rdθdz] – [ρvr + ρ (∂v_r)/∂r dr + vr∂ρ/∂r dr] [rdθdz + dr dθdz]
= ρ [vr rdθdz] –[ρvrrdθdz+ ρ (∂v_r)/∂r rdrdθ dz + vr∂ρ/∂r rdrdθ dz
+ ρvrdrdθdz]
(Other higher order terms are neglected)
= ρvrdr dθdz – (ρ (∂v_r)/∂r + v_r ∂ρ/∂r)rdrdθdz
Or,
Rate of accumulation of mass = – ρvrdr dθdz– ρ (∂v_r)/∂rrdr dθdz
Now,
Rate of accumulation of mass in θ direction can be given by,
Rate of mass enters beρv_θdrdz
Rate of mass leaves be (ρ + ∂ρ/r∂θ dθ)(v_θ + (∂v_θ)/r∂θ dθ)drdz
So,
Rate of accumulation of mass = ρv_θdrdz– (ρ + ∂ρ/r∂θ dθ)(v_θ + (∂v_θ)/r∂θ dθ)drdz
= ρv_θdrdz–[ρv_θ+ρ (∂v_θ)/r∂θ+v_θ ∂ρ/r∂θ dθ+0] dr dz
(Neglecting higher order terms, so we can write zero ‘0’)
= ρv_θdrdz–ρv_θdrdz + (ρ (∂v_θ)/r∂θ+v_θ ∂ρ/r∂θ dθ)drdz
Or,
Rate of accumulation of mass =– (∂(ρv_θ))/r∂θrdr dθdz
Similarly,
Rate of accumulation of mass in z direction can be given by,
Rate of mass enters be ρv_zrdθdr
Rate of mass leaves be (ρ + ∂ρ/r∂z dz)(v_z + (∂v_z)/∂z dz)rdθdr
So,
Rate of accumulation of mass = ρv_zrdθdr– (ρ + ∂ρ/r∂z dz )(v_z + (∂v_z)/∂z dz)r dθdr
= ρv_zrdθdr–[ρv_z+ v_z ∂ρ/r∂z dz+ρ (∂v_z)/∂z dz+0]r dθdr
(Neglecting higher order terms, so we can write zero ‘0’)
= ρv_zrdθdr– ρv_zrdθdr –(ρ (∂v_z)/∂z+v_z ∂ρ/∂z)r dθdrdz
Or,
Rate of accumulation of mass = –(∂(ρv_z))/∂zrdr dθdz
Adding all above equations of rate of accumulation of mass, we get the rate of accumulation of an elementary control volume –
= –ρvrdr dθdz– ρ (∂v_r)/∂rrdr dθdz– (∂(ρv_θ))/r∂θrdr dθdz– (∂(ρv_z))/∂zrdr dθdz
Or,
∂ρ/∂trdr dθdz = – [(ρv_r)/r – ρ (∂v_r)/∂r– (∂(ρv_θ))/r∂θ– (∂(ρv_z))/∂z]rdr dθdz
Or,
∂ρ/∂t = – [(ρv_r)/r – ρ (∂v_r)/∂r– (∂(ρv_θ))/r∂θ– (∂(ρv_z))/∂z]
= –[(∂(〖ρv〗_r))/∂r – 1/r.(∂(ρv_θ))/∂θ–(∂(ρv_z))/∂z – (ρv_r)/r]
Or,
∂ρ/∂t + [(∂(〖ρv〗_r))/∂r+1/r.(∂(ρv_θ))/∂θ+(∂(ρv_z))/∂z+(ρv_r)/r] = 0
This is the three-dimensional Continuity Equation for unsteady compressible flow.
Note:
The above Continuity Equation can be formed for two-dimensionalcoordinate system (r, θ) for different fluid flow-
For Unsteady Compressible Flow:
The equation can be written as-
∂ρ/∂t + [(∂(〖ρv〗_r))/∂r+ 1/r.(∂(ρv_θ))/∂θ+ (ρv_r)/r] = 0
For Steady Compressible Flow:
The equation can be written as,
(∂(〖ρv〗_r))/∂r+ 1/r.(∂(ρv_θ))/∂θ+ (ρv_r)/r= 0
For Unsteady Incompressible Flow:
The equation can be given by,
(∂(v_r))/∂r+ 1/r.(∂(v_θ))/∂θ+ v_r/r= 0
For Steady Incompressible Flow:
Equation should be-
(∂(v_r))/∂r+ 1/r.(∂(v_θ))/∂θ+ v_r/r= 0
Links of Previous Main Topic:-
- Vapour compression refrigeration cycle introduction
- Basic fluid mechanics and properties of fluids introduction
- Fluid statics introduction
- Manometers measurement pressure
- Fluid kinematics
- Lagrangian method for describing fluid method
- Eulerian method for describing fluid method
- Lagrangian relationship from eulerian equations
- Steady and unsteady flows
- Uniform and non uniform flows
- Stream line
- Path lines
- Streak lines
- Acceleration of a fluid particle
- Continuity equation
- Continuity equation in three dimensions in differential form
Links of Next Mechanical Engineering Topics:-