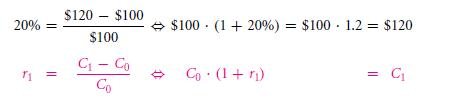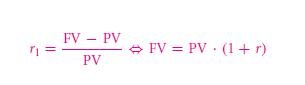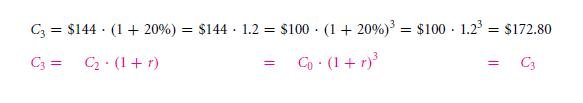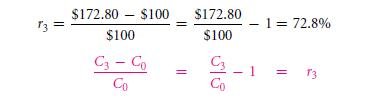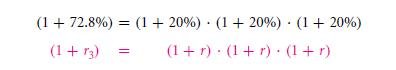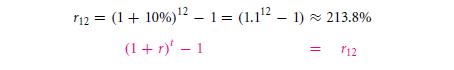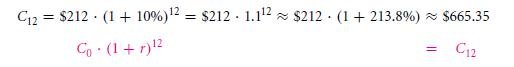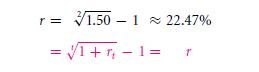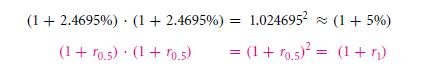As there is a possibility of earning profit by getting the interest returns, any sum of money is more valuable in the upcoming future than its value today. You can always make a deposit that will get your money into a bank account and thus you will get a return back value of the same money but only much greater.
This is the example of a concept called time value of money. It comes rightly up on a dollar is much expensive in the coming time. This is the most simple and crucial concept that you must remember of finance.
2.4A The future value of money
The amount of money that you can get in the future is stated on the many rates of returns that you get, which is of 20% and that too on an investment of $100. Let us turn to the various rate of returns and their formulas (formula no. 2.1) this will determine the money that will be on a grow over he time based on a particular rates of return:
The future value is thus the $120 which will be produced from the $100 that is given today. So, future value sum is a total value of the existential cash amount after it matures. The money time value causes a righteous future value to be that of higher than the present accounted value. We can derive the formula by using abbreviations like FV &PV,
So if we take the subscript r off, it will mean that in one period the interest rate will fluctuate from time 1 which is r1.A time value of money is not a fact that price of goods will change that being caused due to inflation. A time value of money is hence completely based on money that has the capacity to earn interest. A random value of cash is increased to multiple levels in a later time. The next day it is the same value plus the interest that it makes.
2.4 B Compounding and future value
How would it feel if you could earn at the same rate of 20% interest every year that too by reinvesting the money? The 2 hour of return rate – what will it be? One thing is for sure, it will not, be
20% + 20% = 40% for sure!
You know that the $120 that you invested in a year, that you will again invest in a rate of definite return from the first year to the second year.
Hence you are left with,
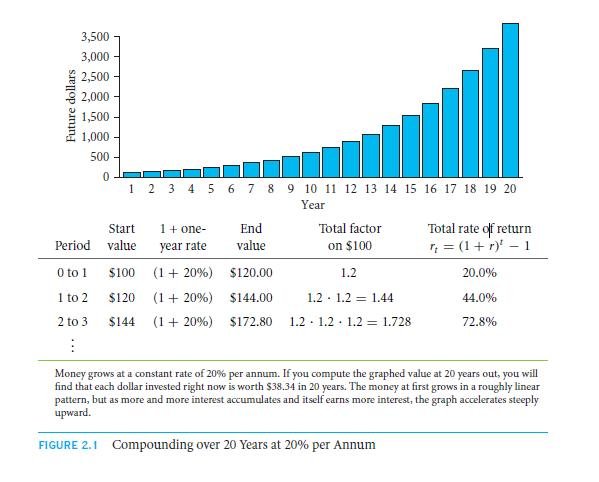
The total $144 is the future constant value of the $100 that is of today – this represents that of a total of two-year duration rate of return which is of,
This stands out to be exceeding the value over that of a 40% as the original total return that is of $20 is in the value of first year and is earned at an additional amount of $4 as interest for the next year. Yes! You will definitely earn interest upon interest! Such a condition or phenomenon is termed as compound interest. In a similar fashion of calculation, the total of three years of rate of returns will be,
This is the calculation of you investing a $144 with 20%.
The rate of return that is for three year is from time ‘0’ to ‘3’ and is to be called r3.
Hence it would be,
This above given formula is assumed as a pack of 3 sequential individual yearly rate of returns into a single holding rate of return for three year duration– this is your earning whether you hold an investment on for a long period or not. The process compounding, has the formula which is referred to as a “one plus formula”:
Or the shorter version,
1.728 = 1.23
The figure below at 2.1 certainly shows pupils how the $100 would be growing if an individual continues in making investments with the rate of returns is that of 20% on a yearly basis. This function of such is exponential – it grows in a preceding rate and is a faster ordeal as the interest grows faster too.
The formula for compounding can be further used to calculate all sort of near or vast future payoffs. Let’s take an example, here and any investment project costs $212 at 10% every year at today’s rate at 12 years and will manufacture an entire holding rate of such returns of,
This $212 investment will turn up to a definite future resembling value of,
Supposedly, you want to know the consecutive two one back to back years of (r) interest rates and will give a total of two year duration of rate of return which will be of 50%. Hence, it will be however not 25%, as the (1 + 25%) * (1 + 25%) – 1 = 1.252 – 1 = 56.25%. Pupils need to solve this one,
(1 + r) * (1 + r) = (1 + r)2 = 1 + 50% = 1.50
Then right answer is,
Check the answer like: (1 + 22.47%) * (1 + 22.47%) = 1.22472 ≈ (1 + 50%). Account the twelve monthly interest rates to be like 213.8%, then what will be the one month interest rate then?
The compounding interestingly works with over a time periods fractional. 5% is the overall interest rate in a year, and if you wish to solve for these rates of return to be over a six month thing. This is so as, (1 + r0.5)2 = (1 + r1), this will compute up to,
(1 + r0.5) = (1 + r1)0.5 = (1 + 5%)0.5 ≈ 1 + 2.4695% = 1.024695
Anecdote
Life expectancy and credit
The life expectancy of yours might be eighty years; however, the thirty year bonds have been existing since that time when the life expectancy in general was only twenty five years. This was on this particular time of the king Hammurabi, which was around B.C.E. 1700 (this great king had established the very first legal system in Babylon, which was the kingdom and is hence famous for this Hammurabi code). Surplus to this, Mesopotamians had solved the financial problems interestingly. A clay tablet that contains all various oldest known to man interest rate problems for all perceivable students of financial arts was also made by them. A student was expected to learn as to the long duration that it takes a silver min a to reach 64 min a at the rate of 20% interest every year. Interest compounds are an answer to the problem of thirty years moreover rather than that on the years 22.81 years. Hence, these will not an easy solvable problem. There is a need for the use of logarithms even.
Check the compounding of 2.4695% over two (six months) period which yields 5%:
Only with the use of algorithms can you determine the period that it would require to take on working with the current rate of interest rate using the same formula. At the interest rates of 3% on a every yearly rate, how lengthy of a duration is going to take to double the money?
Adding or compounding interest rate?
As unfortunate as it can get, the interest rates that are used in the true existing world, marks up as casual deals that sometimes point out to the specific area that they are wrong. Some of the people add on quite a few interest rate instead on compounding. These interest rates, the investments and time duration which are minute and the difference that is created is in between incorrect and correct commutating, which can be a very minor, making the practice of it acceptable even though it is so wrong. Let us take an example; the interest rates being 10% will give a compounding yield of:
This may not be the exact same thing which is as simple as the sum of 2r’s, it however comes up to that of 20%. The great difference that is created is made in between a 20%and also 21% is a “cross term” from r * r. The cross – product that is here unimportant if the rates of returns are small in both cases. Interest rate if stays 1% for both, then that of cross-term will be assorted as 0.0001. It is a small nomination to be that of ignored in all most cases, thus it makes up for a completely forgivable approx value. With a prolonged period of approximation the quality is likely to deteriorate. This happens when you collect and gather many cross-terms.
2.4C How banks quote interest rates
It may surprise you but banks as well as other financial organizations use a wide variety of conventions which are all used in the calculation of interest rates.
The simplest rate of such returns is called annual percentage yield (APY). It is none other than the book term “interest rate”. Banks also call this term as (AER) annual equivalent rate or even that of effective annual rate. For an investment of $100, the APY will be 10%. And, you will remain with the value of $110 on the year’s end.
The total interest rate is stated here without any qualification and is not the rates of return. Rather, it is a simple quoting technique. The real regular interest rate will be that of in division of 365 (or that of 360 in other methods), as it is annual. If for an example, the bank quotes that you get a yearly interest rate quote of 10%. These are daily interest rate which is that of therefore 10% /365 ~ 0.0274%. hence, this will be that of the reason why a bank calls it an annual rate, that is compounded daily. So, when you leave the money in a bank for an entire year, the earning that you get is,
Actual Rate of Returns = [1 + (10%/365)]365 − 1 ≈ 10.52%
In a problem sum, the interest rates of a bank being 10%, will be turned into that of $110.52 as after the time period of one year on the existing value of $100.
(APR)Annual percentage rate, is that of pre-determined rate that requires a quote on the loans that it extends to its customers (in accordance to of 1980’sconsumer credits act). This will be that of the fellow law act requires the borrowers to quote “annual interest rate that is compounded every month”. This renders the APR as an equal number with that of the plain interest rate. Let us take an example, if supposing the quote for you is made as 10% a year, then that means that a lender will be collecting (1 + 10%/12)12 − 1 ≈ 10.47% every year, which is on the entire that has been lent over to you. $100 that you have borrowed, you will get a pay back from the bank of $10.47 on a yearly basis. In a contrast to these various simple interest rates, APR shows different compounding intervals, which are also reflected on other costing such as closing the cost and fees that are derived to help the consumers. Even though the APR is of standardized measure, it is still enough to cause variations that are common in use and are essentially compare tools. It might not be ideal comparing system as it does not always compare apple to apples.
(CD) Certificate of deposit will be better long term investment that makes the ideal stature for a savings accounts deposit of a bank. If the bank wants for a pupil to deposit the sum in a Certificate of deposit, then which interest rate quote will it put? Will it be the interests rate amount quote which is traditional or will it be the APY method? When the main APY will be used for making, it will take up a rate of interest rate 10% quote. Which most of the banks advertise about the APY that is for deposits. In case if you further wish to lend some money from the bank, there will be no loan agreement that will emphasize on the APY. In most times, banks will leave the number to a good print and will focus on basically the interest rate calculation.
Interest rate calculation is not difficult but at point, the calculation can be tiring. The definition is hence bound to this world. The best advice that I can give is that when cash or capital is at a wide stake, if you have a doubt, then ask the bank regarding the interest rate computation. The even better thing that you can do is ask for an illustration of the calculation.
Links of Previous Main Topic:-
- Introduction of corporate finance
- The time value of money and net present value
- Basic scenario perfect markets certainty constant interest rates
- Loans and bonds
- Returns net returns and rates of return
Links of Next Financial Accounting Topics:-
- Present values discounting and capital budgeting
- Net present value
- The capital asset pricing model
- Market imperfections
- Perfect and efficient markets and classical and behavioral finance
- Capital budgeting applications and pitfalls
- From financial statements to economic cash flows
- Valuation comparables financial ratios