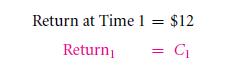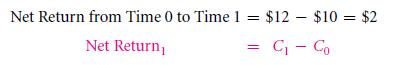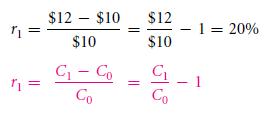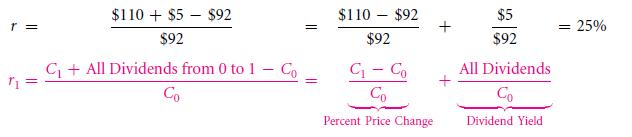Returns, Net Returns, and Rates of Return

Return is the most fundamentally financial concept. The amount value of cash returns that you get in an investment are none other than payoff or return (dollar). Let us take an example, if the probable investment project returns of $12 at a period, then it have

 Time is sub scripted as t. When the time period of 1 is appearing to not be important: it may be denoted tomorrow or the next consecutive month or even the next year. If we denote it at this hour, it is sub scripted as 0.

The total payoff or the net return is summed up as the total difference that is created in the time period which is between the returns that you get and the sort of initial investment that you made. Thus, this deduces that if a project turns out to be negative it is unprofitable and that if the probable project is positive then it is profitable. If for example we take an investment that costs $10 at today’s rate, and returns are made of $12, the time is considered as 1 without anything in between. The net return is $2 in that case. On a general viewpoint, we must use not one but 2 subscripts on the returns – the starting of a particular investment are marked by ‘0’ and the end period is marked as ‘1’. Thus, we get the significance like “net return _0,1.” It ruins the appetite. Doesn’t it? So let us remove and replace the first initial subscript.

 The total rate of return will hence be the percentage expression of the net return of an initial investment that is made.

 Though the convenient method of calculation is denoted as,

 The unique letter r denotes the rate of returns that they get. The percentage is the unit that represents that of the 1/100. Therefore, 20% is basically the same value as 0.20.

Interim payments are a part of many investments. In context to examples, let us consider an example, there are stocks that pay many interim cash coupons, as well as there are the ones that pay cash dividends. There is such real estate investment too that pay off by producing interim rent. So for such complex cases, how is such rate of return calculated? An easy method for this is to simply add the interim payments that are to numerator of the fraction formation. To show how to it done, suppose the investment cost is $92, and it pays a rate of dividend amount of $5 (i.e. on the end period), which gives up the value of $110. The rate of return will be:

 The breaking down of 2 additive parts occurs as there is both intermittent and final payment which is included. The various price changes or the supposed all capital gain hence is the first part is essentially the difference that is noted in between the buying price and selling price or the ultimate final price, that too without counting the interim payments. These capital gains will hence be noted as the difference that is noted for between the two prices $110 and $92. The price hence is $18. As it is quoted as the percentage of this particular price. The percentage hence would certainly be $18/$92 that are 19.6% in this case. The most second part that is received as an amount is called interim payments. This amount is basically a dividend or rent, and in this particular case is $5. Dividing it into price gives birth to many names such as, current yield, dividend yield, coupon and or, rental yield. These all are stated in percentages. In the example that we are displaying before you, the coupon yield will be $5/$92 which is equivalent to approximately 5.4%. If such interim yield is perceived of a high value, then you may be in a state of negative value of capital gain experience and yet have a solid positive value for the rates of return.

Let us take an example, the cost of a bond is $500 and the coupon that you get for it is $50. It further sells off for $490, and is suffering from a certain capital loss that is $10 in value. This makes the capital yield to be -2%. However, the various rates of returns will be that of 8% [($ 490 + $50 – $ 500)/ $500]. Thus, this states that you are often to work with the rate of return and not the capital gains. This is the only exquisite exception is in the case of working with taxes. This is further because of the way IRS treats interim payments differently from capital gains. (That portion will be further discussed in the Section 10.4.)

The rate of return is a big word thus, in maximum of time; the general people abbreviate it into calling it as simply return instead of net return. Let us take an example; the return that is offered on a $10000 stock purchase is 10%, so this means that you do not receive a unit less 0.1. What it means is that your stock purchase of $10000 is actually giving off rate of returns which is 10%. This is a scenario where the situation is benign. For the reason that a listener will understand the real meaning from your words.Compared to this situation, the more harmful potential that this coupon yield makes in the place of rates of return. It is noticed to be misused more often as, it is the certain shortcut that is lead on for the dividend yield (the stock and bond provided percent payout.) thus, if an individual says that the stock is 5%, then many listeners might interpret the meaning as they had earned an entire rate of return, i.e., 5%. However, others may reach to the conclusion that it means that the stocks paid a 5% coupon yield.

The interest rates must be positive, that is logically. One can always get to earn a 0% even if the money that you possess is kept under a mattress – with that you end up eventually with a large sum of money for the next period that you have of this definite period. Why must you give your equity to someone who will only supply you with a percentage less than that of 0% money that you get in the near future? Interest rates which are thus always positive – with some rare exceptions where both the factors are completely bizarre and mostly trivial.

There is another problem of language: “the most interest rate is leveled up and increased by a total of 5%” – what does this mean even? It could possibly mean that either a previous remaining interest rate let’s assume 10% increased from ten directly of 10% * (1+5%) = 10.5%. This may even be that it increased from 10% to 15%. It is quite unclear because the most basis point units are invented in this situation. Basis points are simply 1/100 of any given percentage. Thus, when a pupil states that the interest rate increased up to 50 basis point, then you can definitely means that the prevailing or existing interest rate will be increased right of the value. That means that is for 10% to 10.5%. In that point if one pupil is able to state that the interest rate increased by 500 basis points, then it means that your interest rate definitely increased right from 10% – 15%.

Important: basis points are known to avoid all “percentage ambiguities”. So, 100 basis points make up 1%.

 Anecdote

Interest rates over the millennia

The interest rates that were used in the ages that can be safely credited as historical are very fascinating. This is probably because of the fact that they look similar to the interest rates that are portrayed today. The typically pursued interest rates are that of the ones which are displayed today ranging from 2% – 20%. It depends on multiple other factors as well. The entire concept has existed since a very long time about over a time period of 2,500 years ago. In the 13^th century B.C.E. right up to 6^th B.C.E.century, the regular interest rates have been approximately 10 – 25% annually; this is the account of Babylonia and Sumer. However, a 20% was fixed as these legal maximum was. In the ancient period of Greece, about 6^th B.C.E.century, the interest rates had been about 16% to 18%. These rates dropped steadfastly about 8% that is by a turn to the millennium. The scenario in the ancient Egypt was not very different with the interest rates being about 10% to 12%. 8% interest rate was the starting of the long list of set percentage in the capital of ancient Rome. This was the case in 5^th B.C.E. century However, this started changing with an increase in the interest rates up to 12%. This was the scenario of the 3^rd A.C.E. century – the time of upheaval. In the middle ages the lending resume was made up to 50% on a yearly basis in England. The rate for the rest of Europe was however, 10% – 20% for the remaining of Europe. When renaissance came, the commercial loans rates fell down to a level of 5% – 15%. This was the situation in Italy, as well as France and Netherlands. English rates were dropped by the 17^th century to 6% to 10% for the first month. The second month came on to be 3% to 6%. The mortgage rates appeared to be down in such a condition. The Dutch and French loan interest rates, which were of 4% to 5% financed the American revolution.

Links of Previous Main Topic:-

• Introduction of corporate finance
• The time value of money and net present value
• Basic scenario perfect markets certainty constant interest rates
• Loans and bonds

Links of Next Financial Accounting Topics:-

• The time value of money future value and compounding
• Present values discounting and capital budgeting
• Net present value