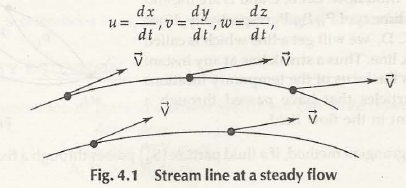
Streamline is the flow of fluid where velocity remains constant at very fixed point. In other words, if the velocity vector is tangential to fluid flow curve, it is called streamline as shown in Fig. 4.1
Let us consider u be the velocity in x-direction
v be the velocity in y-direction
w be the velocity in z-direction
It can be written as
u = [dx/dt]
v = [dy/dt]
And,
w = [dz/dt]
The equation of general stream line can be given by,
dx/u = dy/v = dz/w
For two rectangular coordinates, the above equation can be written as-
dx/u = dy/v
Note:
The above equation shows that slope of each stream line is equal to the ratio of respective velocity.
Links of Previous Main Topic:-
- Vapour compression refrigeration cycle introduction
- Basic fluid mechanics and properties of fluids introduction
- Fluid statics introduction
- Manometers measurement pressure
- Fluid kinematics
- Lagrangian method for describing fluid method
- Eulerian method for describing fluid method
- Lagrangian relationship from eulerian equations
- Steady and unsteady flows
Links of Next Mechanical Engineering Topics:-
