Coefficient of Restitution can be defined as the measure of amount of energy lost during the deforming of two collided bodies or how much kinetic energy remains rebound after collision.
For elastic bodies, Newton’s law of collision states that velocity of separation of bodies during collision tends to have constant ratio to their velocities after collision. Coefficient of Restitution (e) is the constant of proportionality.
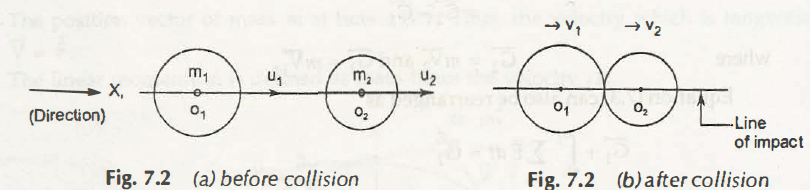
Let us consider two bodies of mass m1 and m2as shown in figure below,
Initial Velocities are u1 and u2 and final velocities are v1 and v2 respectively
Thus,
Relative velocity before collision = u1 – u2
Relative velocity after collision = v2 –v1
According to Newton’s law of collision of elastic bodies,
Coefficient of Restitution, e = (v2 –v1)/ (u1 – u2)
Some of these conditions are applied for different types of bodies-
- e = 1 (For perfectly elastic body)
- e = 0 (For perfectly plastic body)
- 0 < e < 1 (For general elastic body)
Note:
For inelastic bodies, this transformation of energy deforms into various forms such as heat, sound, etc. Thus, the kinetic energy does not rebound and loss of kinetic energy can be given by
Loss in Kinetic Energy = Total Kinetic Energy Before Impact – Total Kinetic Energy After Impact
Example 7.1:
A ball of mass 2 kg strikes another body of mass 4 kg with a velocity 4 m/s. After collision the first ball comes to rest. Determine the velocity of second ball and the coefficient of restitution.
Solution:
According to conversation law of momentum,
m1u1 + m2u2 = m1v1 + m2v2
Given Data:
m1= 2 kg
u1 = 4 m/s
m2= 4 kg
u2 = 0
v1 = 0
v2= ?
Substituting all the values, we get
2 x 4 + 4 x 0 = 2 x 0 + 4 x v2
Hence,
v2 = 2 m/s
Now,
Coefficient of Restitution will be,
e = (v2 –v1)/ (u1 – u2)
Substituting all values from the above given data,
e = (2 – 0)/ (4 – 0)
= 0.5
Note:
We can see that the value of coefficient of restitution is equal to 0.5. It means that it is for elastic object i.e.,ball.
Example 7.2:
An object of mass 1 kg strikes another ball of mass 2 kg with an initial velocity of 2 m/s. If the first body has u2 = 0, then calculate the magnitude of final velocities of both the objects. (Take coefficient of restitution = 0.5)
Solution:
We know that:
m1u1 + m2u2 = m1v1 + m2v2
Given Data:
m1= 1 kg
u1 = 2 m/s
m2= 2 kg
u2 = 0
e = 0.5
v1= ?
v2= ?
Substituting all the values, we get-
1 x 2 + 2 x 0 = 1 x v1 + 2 x v2
v1 + 2v2 = 3 —————————- (1)
Since,
e = 0.5
(v2 –v1)/ (u1 – u2) = 0.5
(v2 –v1)/ (2 – 0) = 0.5
v2 –v1 = 1
Hence,
v2 =v1
Substituting the value in equation no. (1), we get-
3v2 = 3
v2 = 1 m/s andv1 = 1 m/s
Links of Previous Main Topic:-
- Position vector velocity and acceleration
- Plane kinematics of rigid bodies introduction
- Combined motion of translation and rotation
- Rectilinear motion in kinetics of particles
- Work and energy
- Linear momentum
- Linear impulse
- Conservation of linear momentum
- Direct collision of two bodies
- Oblique collision bodies
Links of Next Mechanical Engineering Topics:-