The addition of vector represented the way forces and velocities combine. Suppose, a car is travelling in north at 20 miles per hour and a kid is in back seat behind driver throws any object at 20 miles per hour towards his sibling who is sitting in east direction, then velocity of any object will move in north-easterly direction. Through velocity vector, you will find that a right triangle is obtained, and in such a case the total velocity is hypotenuse.
Therefore, the magnitude of velocity vector which signifies total speed of object is √202+202 = 20√2 miles per hour.
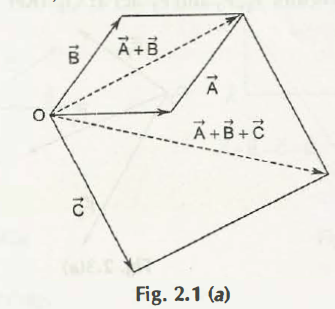
There are two important properties that are related to addition of vectors:
- The communicative law that represents order of addition which does not matter:
a + b = b + a
This law is said to be parallelogram law. There are two edges of any parallelogram that defines, a + b and other pair of edges would define as b + a. This helps to retrieve both sums as equal which is similar to diagonal of parallelogram.
- The associative law which help to gain the sum of three vectors that would not depend on which pair of vector is added in first option:
(a + b) + c= a + (b + c)
Links of Previous Main Topic:-
Links of Next Mechanical Engineering Topics:-