Definition:
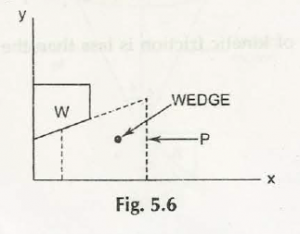
A block or small piece of mass with unparalleled faces, especially two of them being opposite to each other are known as wedge. The application of this wedge is particular in lifting other blocks. The horizontal force used by this wedge or P in the figure below is capable to lift weight of W. The power applied to uplift that block should always be greater than W, only then it will create a counter upward power to help in the uplifting.
Let us consider this figure for the definition and description mentioned above:
Here are some examples and solutions:
The force Pis applied to a block of mass 9 Kg, which is stationary before the force applied. Determine the magnitude and direction of the friction force F exerted by the horizontal surface on the block if (a) P = 30 N (b) P = 40 N (c) P =50 N. (Re( Fig. 5.l(a)).
Solution:
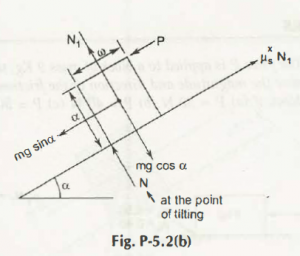
Consider these two figures:
From there we are coming to:
µs N 1 – mg sin α — P = 0
Ʃ FY = 0
N1 –mg cos α = 0
From (1) => p= µS N1 – mg sin α
= µS (mg cosα ) -mg sin α
We will now check the condition Just Before Tipping
Taking moment about A
Ʃ MA = 0
P x d + mg sin α x d /2 – mg cos α x w /2
Substituting the value of P from (3),
Mgd (µScos α – sin α) + mgd .sin α /2
= mg cos α x w /2.
We can also go for:
d (µScos α –sin α + sin α / 2)
= cos α x w/2
Or there is another:
d (µScos α –sin α + sin α / 2)
= w .cos α /2
And there is also:
d/(1) = (cos α/2)/ (µScos α – sin α/2 )
Or simply by proving that:
d/w = 1 / 2µ =tan α
Example:
Find the least force required to drag a body of weight W, placed on a = Wrought inclined plane having inclination a to the horizontal. The force is applied to the body in such1 a way that it makes an angle θ to the inclined plane and the body is (a) on the point of motion up the plane (b) on the point of ‘motion down the plane.
Please consider this figure:
Ʃ FX =0
P =cos θ – W sin α – µ N =0
P cos θ =W sin α + µN
Ʃ FY =0
N +P sin θ – W cos α = 0
N = W cos α – P sin θ
Substituting the value of N in (1), we are coming to
P cos θ = W sin α +µ (w cos α – p sin θ )
P cos θ = W sin α +µ w cos α – p sin θ
P (cos θ = µ sin θ) + W (sin α + µ cos α)
P = W (sin α + µ cos α) / cos θ + µ sin θ
=W (sin α + tan ϕ cosα ) / (cos θ + tan ϕ sin θ)
= W (sin α + sinϕ/ cosϕcosα) / (cos θ + sinϕ/ cosϕ sinθ)
= W (sin α cos ϕ + cos α sin ϕ ) / (cos θ cos ϕ + sin ϕ )
= W sin (α + ϕ) / cos (θ – ϕ)
P will be minimum when cos (θ – ϕ) is maximum i.e.; cos (θ -ϕ) == 1
i.e., θ =ϕ,
p min = W sin (α +ϕ) .
Ʃ FX =0
P cos θ + µN – W sin α = 0
W sin α = p cos θ + µN
Substituting the value of N in equation (3), we are getting
W sin α = p cos θ + µ (w cost α – p sin θ)
W sin α – µW cos α = p cos θ – µp sin θ
= W (sin α – µ cos α) = p (cos θ – µ sin θ) / cos θ – tan ϕ sin θ
= W (sin α cos ϕ – cos α sin ϕ ) / (cos θ cos ϕ – sin θ sin ϕ)
P = W sin (α –ϕ) / cos (θ + ϕ)
W (sin α – sin ϕ/ cos ϕ cos α) / (cos θ – sin ϕ/ cos ϕ sin θ)
Example:
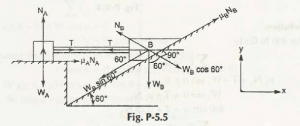
Two blocks A and Bare connected by a horizontal rod and are supported on two rough planes as shown in Fig. P-5.5. if the weigh t of block B is 1500 N and coefficient of friction of block A and B are 0.25 and 0.35 respectively, find the smallest weight of block A for which equilibrium exists.
Solution:
Consider this figure:
First, for block A:
Ʃ FY =0
NA = WA
Ʃ FX = 0
T +µA NA = 0
T = – µA NA
= – 0.25 x WA = – 0.25WA
Second, for block B:
Ʃ FY =0
N B –W Bcos 60° + T sin 60° = 0
Ʃ FY =0
-WB sin 60 + µB NB – T cos 600 = 0
– 1500 sin 600 + 0.35 NB – T x ½ = 0
-1500 sin 600 + 0.35 (WBcos 600 – T sin 600 = T /2
[Substituting NB from (3)]
1500 sin 600 + 0.35 x 0.35 x 1500 cos 600 -0.35 x T sin 600 = ½
[Using eqn( 1) and (2)]
– 1036.54 = 0.80 T,
T = – 1295.7.
WA = – T / 0.25 = + 1295 .7 / 0.25 = 5182.8 N
Links of Previous Main Topic:-
- Introduction to statics
- Introduction to vector algebra
- Two dimensional force systems
Moment - Introduction concept of equilibrium of rigid body
- Friction introduction
- Coefficient of friction
- Angle of friction
- Cone of friction
- Static friction and kinetic friction
- Coulomb friction
- Angle of repose
Links of Next Mechanical Engineering Topics:-