A body will rotate on an axis when as a result of a force action. This axis does not intersect with the line of work, and neither is parallel to the line of action of the force.
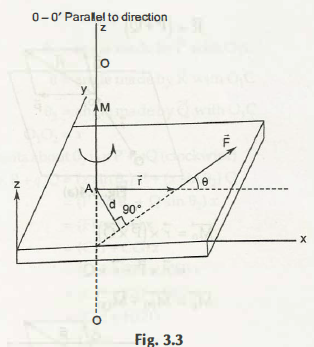
In the figure given below it shows a body on which the force F is acted on. (0-0) Is an axis which is at a right angle to the body. D is the distance between the lines of action of force from the axis. The magnitude of the moment is the product of the force and the perpendicular distance.
Therefore we come to a conclusion that M = F d
If the moment is anticlockwise, then the sign is taken as positive, and if the moment is made as anticlockwise, then it is considered as a negative sign. This sign convention will help you to remember the signs quickly without getting confused.
So here M is positive. Now we will apply this on the vectors to determine the moment of force.
Here we see that the moment F is about the point A the passes by the z-axis and is represented by the cross product.
However here r is the position vector which arises from the moment reference point A and is placed on the line of action F. The magnitude | M | = M = F r sin = F r, sin θ =f= r sin θ do not get influenced by the particular point on the line of action F which is directed towards the negative vector.The direction of M can be easily directed by the right-hand screw rule to the sequence.