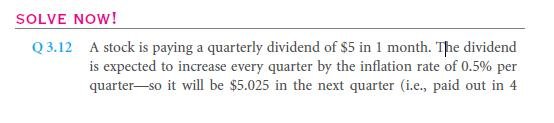Perpetuity is simply described as the project that will serve a constant cash flow and will keep on repeating itself forever. In case if cost of the entire capital is held as a stagnant and thus total amount of capital grows over at the steady rate, then perpetuities can lend themselves like a speedy present value solution. This is a very basic rule that helps in the estimation. Even though these formulas seem very intimidating on the very first look, the use of it becomes a quickly learned and accepted thing.
3.1 A the simple perpetuity formula
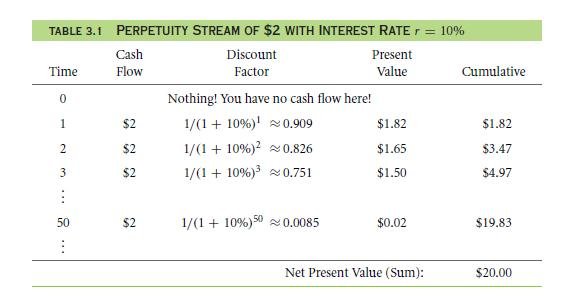
With a constant unchanging interest rate which is 10%, what do you think, how big a value is to be invested at the present market to receive a similar dollar value of the interest that gives $2 every year? The table no. 3.1 will showcase the current present values among the future payments which have the perpetuity of $2 for an eternity with the interest rate of 10% every year.
Notice how the payment that is made at the time of 0 is. Also notice that payment of an individual becomes smaller on the outwards.
The perpetuity net present value can be $20 if you have the will to wait for an eternity to sum up the many uncountable numbers. Though when you will be using a spreadsheet, then you can put and add the initial fifty terms which are there in the first, and then you get the PV that is of $19.83. When you sum up the 50 first terms, then you get the PV that is of $19.9986. Calculatedly, the sum will make up for the $20 sharp. The reason for such will be because there will be a shortcut method available to compute the total present value, capital cost of being constant.
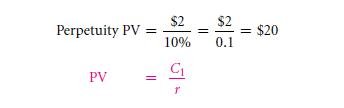The time ‘1’ is the subscript used in the above given formula. This is to make remind of the very first cash flow which never occurs in the present time, but in the following year – cash flows will remain as of the exact amount for the upcoming consecutive years.
ANECDOTE
The Oldest Institutions and Perpetuities
Assumption of that projects will last a life time is what perpetuities are. However, nothing lasts forever. This is the oldest western institution is Catholic Roman Church and is 2000 years old. And oldest corporation that exists is of reformed greatly as a protestant church for the Dutch in the New York City in United States. This place was formed in the 1628 and was granted a charter by King William in the 1696. Canadian Hudson’s bay firm was established in the year 1670 which is the acclaimed oldest company that is continuous on going incorporation.
The naval base in Guantanamo is leased in 1903 from Cuba from United States as a perpetuity in exchange of 2000 pesos every year in U.S. gold. This sum was equivalent to a sum of $4085. Fidel Castro had once restated time by saying “whatever is indefinite lasts 100 years”. Anyway, Cuban government will not recognize the agreement as a valid one and this does not accept that many payments that are made annually. However, they were right on not expelling the Americans either. Which itself is a wise move.
This is in fact the most easy way to get accustomed with the perpetuities and to solve problems.
3.1 B The growing perpetuity formula
In place of the equal value of cash, what if the cash flow expand in number with the progressing time? The formula for growing perpetuity allows maintaining a fixed and unchanging rate g for a certain period, and gives a less interest rate. The table 3.2 displays the increasing perpetuity which pays $2 in the upcoming year, with a growth rate – 5% and the cost of capital 10%. The PV of the initial 30 terms will sum to give $30.09. First of the 100 terms will give the value of $39.64. Initial 200 terms will be $39.98. Hence the formula will be,
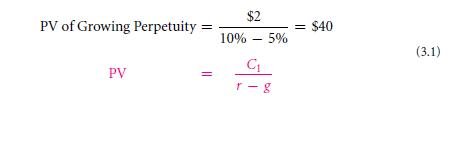
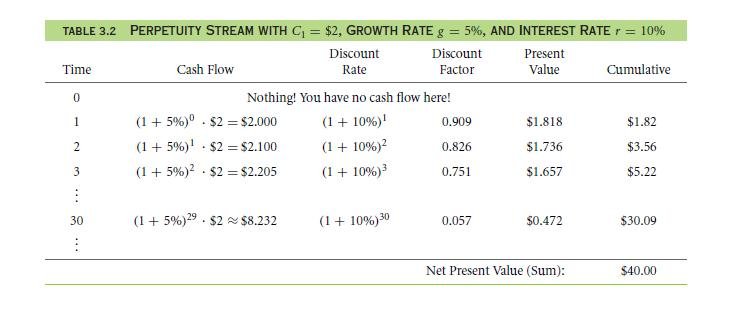As the ‘1’ subscript indicates the cash flows being in the coming session and is not necessary as the entire pattern of cash flows is different than the initial one. The existing interest rate is the one which reduced by the exponential growth rate that is of the cash flows. The coming table shows the initial application that you make in the growth of one year. Hence, a cash flow is discounted to (1 + r)30 however, it is multiplied by the growth factor (1 + g)29. You will be encountering applications of growing such perpetuity formula. Let us see an example, common assumptions are made in cases of rate of inflation by the cash flows. You will be using the formula later to obtain the associative yet important values in this book. The design is called pro formulas.
You must be careful in using cash flow the upcoming year as numerator in any formula. Subscript ‘1’ is to remind that to you. Let us proceed with an example, when you wish to use the formula all on your own firm it earns $100 million in the present year with an expectation to continue growing at 5% rate for eternity, the cash flow then must be in the specific numerator as $105 million and not simply $100 million.
What if a cash flow grew at a faster rate compared to that of interest rate, then? The formula would indicate value that is negative PV. This is for the scenario that would be nonsensical. The PV is less than infinity in the perpetuity formula and will be lesser than the boundary of infinity as the present dollars for each term is a of the previous time period. If the g was greater than the r cash flow for a year later will be more than that of today’s price. With an example, the discount rate being 10% growth rates of all cash flows g = 15%. This is the initial set of cash flow will be $2 * 1.15 = $2.30 and will discount up to $2.09 at the present market. Second of the cash flow will be $2 * 1.152 = $2.645 which will give $2.186. Present available value of the cash flow will be higher. Infinite numbers will increase the yielding of infinity as a value. Infinity value is not sensible and has a definite sum of money that can be used. Thus, growing and perpetuity formula will give rise to the negative value only if, g ≥ r like it should.
3.1C Perpetuity application: stock valuation with a Gordon growth model
With fixed interest rates and the growth rates which are the external payment requirement, the perpetuities that are correctly placed very rarely. These can be helpful for a back to envelope estimate. Consider a business that is both mature ad stable along with $1 million profits the coming year. As the company is stable, the profits are expected to grow on inflation rate of 2% every year. The meaning is deciphered that the company is going to earn the value of $1,020,000 at a time span of 2 years. For 3 years, it will be $1,040,400. The firm will be facing a certain capital cost that is 8%. This suggests that the firm should be more worthy than what it is,
In the true life there is going to be many uncertainties in the significant life: the upcoming years profit may not be same to this year, the growth rate of a firm may be different from the previous one or, capital cost may be different too. Hence, the $16.7 million must be considered as a fast-and-dirty approximation. This may even be considered as the upper limit.
The growing model is directly applied in most times to any stock market. If you have the believe that the stocks dividends will all grow up to 5% for eternity, and pay a dividend of 10% and one expect the dividend to be $10 the coming year, then this would be the stock price at the current date,
Would be absolutely correct. The growth of the perpetuity is often termed as the renowned Gordon growth model, in honor to the inventor, known as Myron Gordon.
In the year of 2004, yahoo finance listed the firm General Electric as the one having a certain dividend yield of the rate 2.43%. Dividends when divided by stock price, i.e., D/P are dividend yield. So, let’s rearrange the formula of 3.2:
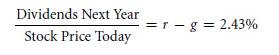Hence, you can understand that all of the real existing market believes on an definite cost capital for firm General Electric will exceed the growing rate of the dividends by 2.4%. Yahoo further links a small summary of the GE that will pay $7.643 billion as in the dividend of a year in the year 2003 & $6.358 billion on the year 2001. Over the course of two year, growth rate will be around 9.6% every year ($6.358 * 1.0962 ≈$7.64). Thus, if you think that there can be 9.6% per year, then there can be a good representation that too of the total future growing rate of the dividends. All financial markets will value the GE as if,
Assuming, this being a prominent factor in the world of finance. To loosely speak, cousins of all various cash flows are the corporate stockholders. Hence, you can think of a certain value of present stock as the total worth of the earning stream that will give the product. Recall this from chapter no. 1, about the owners receiving the dividends and cash flows, which is paid out as the later one. (In the chapter 13, you will be explained about these earnings in a more detailed manner.) This is more common issue to assume that value of a firm is,
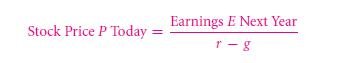Hence, on the journey of determining the rate of return, investors need (cost of capital), a current stock price, that the everlasting growing rate of the earnings. Yahoo finance shows us the required information again. GE was listed as ‘trailing P/E’ ratio by them. Calculative current stock value of the price dividend will be by the historical earnings which is 21. The listed ratio is however, is calculated similar to the price which is divided as one of current earnings growth rate which sums up to 18.5. This perpetuity formula for growth which is to bring the concepts closer. Yahoo finance is to tell that the GE’s earnings are of a growth rate which is 6.3%. Then the g that is in the given formula will let you assume the current earnings growth rate which is a long term thing of growth rate. All that you need to do to rearrange this formula of the return rates:
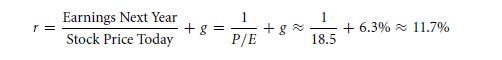Looking at the GE’s P/E ratio, and the growth rate, investors expect the rate of return to be that of around 12% on a yearly basis.
You must understand that these are approximated rates, which shouldn’t be taken seriously at all. The accuracy is not a very important factor. The GE of a brand will not be lasting forever, so, the earnings aren’t that of the cash flows that need to be there. The numbers that are given are not at all uninteresting and discount rate is that not constant.The earnings that will not be growing at that 6.3% forever. GE is greatly a very steady firm who is mostly to be there for a far too off time. You can do that lot bad than to assume that with a capital costs, the GE ownership will be around 12% yearly. It might rather be somewhat around 10% to 14%.
Links of Previous Main Topic:-
- Introduction of corporate finance
- The time value of money and net present value
- Stock and bond valuation annuities and perpetuities
Links of Next Financial Accounting Topics:-
