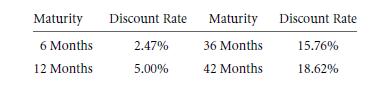
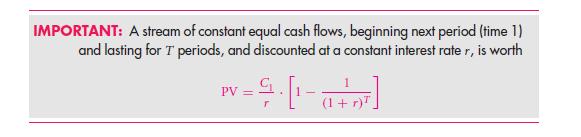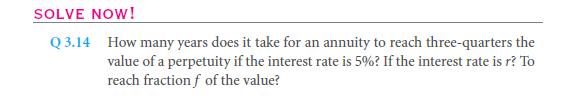The next categories of such cash flow streams will lend a go to kind of quick formula as an annuity. It is defined as the stream of cash flows which are given for a number of definite periods. Very different from perpetuity, the payments will hence stop after the transition of T period. Let us take an example, suppose, if interests rate is that of the 10% for a period, then what will be the entire value of any annuity that will pay $5 for every period for the upcoming 3 years?
So let us take this this way, so that you can calculate the total amount of net present value,
Annuity of the formula makes the work short for the NPV calculation,
This is a shortcut – really? This may not be that for a total of three periods, though we can try to have a 360 period annuity – what can sum up as the preferred method then? Anyone works right?
ANECDOTE
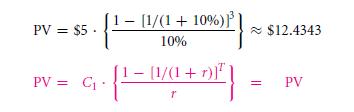
Fibonacci and the Invention of Net Present Value
It is argued by William Coetzmann, that the famous Leonardo of Pisa, was commonly known as Fibonacci. The man who invented the very famous undoubtedly successful “Fibonacci series” may also be known as a concept of the net present value.
Fibonacci’s family was that of the merchants who were in the Mediterranean on the 13th century. They used to trade relations with the Arabian merchants of the northern African lands. He wrote about the mathematics that was the primary used tool that solved the problems merchants faced. This was in the effect to the understanding of the goods pricing and the currencies that are relative to each other. Just imagine how rich could you get this result if in case you had the determination of the competition in the goods that were more related to the others faster. You can consider of Fibonacci along with the Pisan merchants as financial engineers of the 13th century.
Fibonacci had written this in the most exclusive famous treatise method, which is the liber abaci that too at the age of 30 and it was published in 1202. Everyone all are still looking and working on the same kind of problem sums at the present date – this he had predicted. The solution that you solved for the Q 3.17 which is known as the “On A Soldier Receiving 300 Bezants For His Fief”:
The king grants an annuity of 300 bezants every year to a soldier. Which he pays back in quarterly installment that is of 75 marvelous bezants. Thus, king later will alter the payment fixed schedule up to a yearly end of the year payment that is of 300. Solider will be able to then earn a 2 bezant on a value of 100 per month in investments. So what is the effective compensation that exists that is only on the end of the terms of the annuity changing way?
You must learn as to how the calculation of the value of the payments at various different points to solve the problem. The total time value of the money must be understood. What will be the worth of 75 bezants that too in a 1 or 2 year quarters? What will thus this value of 300 exclusive bezants be in these years? So, yes, the money is more worthy earlier than later. You must always determine the value of it to see how much is in the order. As to how the order is bad or good for this king & or the soldier. The interest rate must be used to determine this. Then you further need to compare the cash flows. Plus in addition to this, the original schedule is good or the revised one is better? This is in the terms of common denominator. The common denominator is the one that will remain the same in both the streams’ present value.
3.2 A Annuity application: fixed-rate mortgage payments
Most of the mortgages have fixed-rate mortgage loans, which are therefore basically annuities. The promise is made that of a basic equal cash payments that is given each month top the money lender. The thirty year mortgages with specific monthly payments are that of 360 payments in the annuity. What will be the monthly payment that you have to make in case you took a total of thirty year lease loan of the sum $500,000 with and that too with the interest rate which is 7.5% yearly?
Just before proceeding, all that you essentially need to understand is that this is a little bit more institutional knowledge in this place. Mortgage arrangers are like the banks. They quote all the interest by simply dividing a lease quote by twelve. So, if the rightful monthly interest will be 7.5%/ 12 = 0.625%. If not compounded, the month basis interest rate will be the value of (1 + 7.5%)1/12−1 ≈ 0.605%.
A thirty year rent lease is of a total annuity sum with the 360 payments of the equal value, and that too with the discount rate of 0.0625% every month. The PV is $500,000 which is that sum of money that one will borrow. The annuity is that of the value of the value:
With the solution to the cash flows, you can get hold of the monthly payments that you get on the mortgage of $500,000/143.018 ≈ $3,496.07 that is for the 360 months.
3.2 B Annuity application: a level-coupon bond
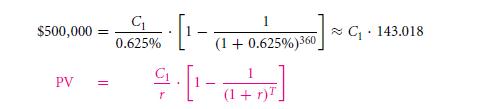
Exercise the newfound knowledge with an elaborate example, with the bonds. Let us recall that the bond is of a proper financial claim that is sold by government. It may also be sold definitely by a firm. A bond comes in many variations, with only useful classifications can turn them into a couple of coupon yield bonds and the zero-bonds or zero coupon bonds. The holder is paid cash buy a couponyield bond and that too at most different intervals of time. The zero bonds will always pay the amount at a single amount of money on its maturing term. Many of the coupon bonds pay the regular coupon value which is similar to that of the rates of interest that is prevailing at that very time of original sale of a bond and always returns to the “principal amount” which is further added final coupon which is produced at the very ending term of any given bond.
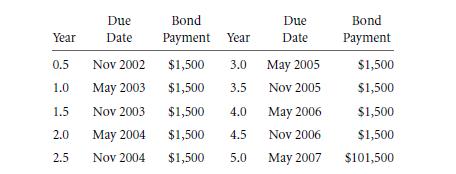
Take an example, and assume that the coupon bond will be paying $1,500 every 6 months for a period of 5 years. Along with the additional amount of $100,00 of course. This pattern will be so common with features which are absolutely stunning: bond with the very coupon that remains for the rest of the bond’s shelf life that is named as a level coupon bond. These sort of bonds will be of the most attractive common type of bonds that rein the markets. This is $100,000 is the principal which is in contrast with a value of $1,500 half yearly coupons. These bonds are most commonly named as by adding up the most coupon payment that is about over the period of 1 year. And this divides the sum of coupon payments (annual) by the total principal. Hence, this bond should be called as the “3% semiannual coupon bond”. Now taking that the “3% semiannual coupon bond” will be as a named convention that is for the bonds for a specific pattern of cash flow – the rate of interest is that anyone would expect if anyone had to make a bond. In the section of 2.4B there were given names for designations of interest quotes and with the distinct interest rates. Even though the bond costs $100,000 at the present market, then the rate of interest will be that of the 3% rate for every year. But, the rate will actually be 1.0152− 1 ≈ 3.02% on a yearly basis.
Then, this $100,00, will be selling for a total of 3% rate that is the semiannual coupon bond then? This will come on a defined promised payment pattern:
The second thing that everyone needs to determine is that whether the arts of returns are to be applied to the cash flows. Looking at the example at hand, there is an existential interest rate is that of a total 5% on a yearly basis. This further translates to 2.4% for the upcoming 6 months and is 10.25% on a time period of two subsequent years. Thus it goes on.
Lastly the compute factors of discount is 1/(1 + rt) = 1/(1 + r)t , thus this will be multiplied by the value of each of the future payments. This will further give a certain present value of the bond payment. You can hence calculate and put together the overall worth of a bond:
You must know that the various amounts that is to be expecting is that of the rate 3% and is semi-annual in the level of the coupon that is to be traded. The amount that is needed for trading is that of $91,501.42 in the absolute perfect market. The present current price that is made is that of a bond that is represented below. The current existing price of a bond is of the final ultimate principal payment on the price given of that $100,000. The bond in trade is said to be at a definite discount rate. The opposite of this value would be referred to as a premium.
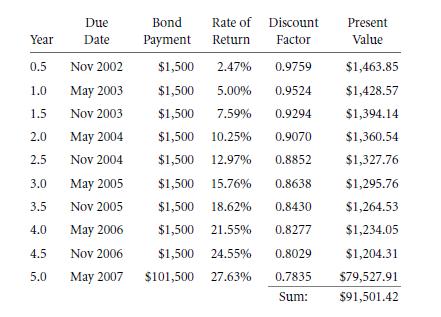
The bonds value can also be calculated by quickly by using an annuity formula. Let us go on ahead to make the 6 month period work. The 10 such coupon cash flow that was liberally used $1,500 at an interest rate, which is of a 2.47%. In accordance to the formula, are that of 10 coupon payments which are worth.
To add to this formula, you will get a $100,000 repayment on the principal, the years that are used to denote the 5th and is the worth,
The total present value of the bond will hence sum to a total of $91,501.42. Important remainder of the quotes versus the returns: you must never let it confuse a bond’s authority with the authentic interest that is paid. The 3% of the semiannual coupon bond that is the slightest just designation for the payout pattern of the bond. The bond that is formed is not to be given up on coupon payments and is mostly equal to the 1.5% on the previously made of $91,501.42. The interest rate that prevails is not associated with a quoted interest rate which is on the existing coupon bond.
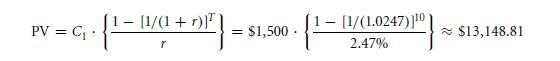
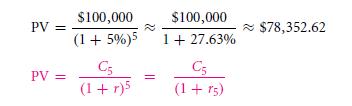
All that you need to determine is that whether the value is that of 0% coupon bond / 10% coupon bonds the prevailing economy wide rate 5%. Saying this is just like saying that the real- life world is that of many corporations who just simply choose to keep similar rates to the existing interest rates. The moments of such inception is therefore momentary and also neither of the premium or the discount that exist. The one brief issue that is instant is the instant coupon rate and that of the economy – wide and broad interest rate is actually pretty close. Though the after insurance and market of interest rates are to move and circulate around with the bond payments being fixed and designated with the coupon name of the bond.
Links of Previous Main Topic:-
- Introduction of corporate finance
- The time value of money and net present value
- Stock and bond valuation annuities and perpetuities
- Perpetuities
Links of Next Financial Accounting Topics:-
- The four formulas summarized
- Projects with different lives and rental equivalents
- Perpetuity and annuity derivations
- Comparing different multiyear contracts
- Capital structure patterns in the united states
- Investment banking and mergers and acquisitions
- Corporate governance
- International finance
- Options and risk management
