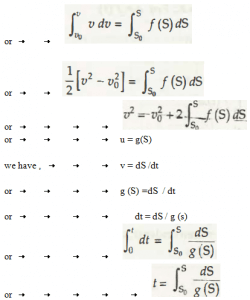In equation 1.5.1, a = f (t)
This states acceleration which is a function of time.
Taking from the equation (1.2),
dv / dt =a = f (t)
Or calculation for dv = f (t) dt
On integrating it, the calculated equation is,
In equation 1.5.2, a = f (v)
This states acceleration which is a function of velocity.
Taking from the equation (1.3),
a = dv / dt = f (v)
Or calculation for dv / f (v) dt
On integrating it, the calculated equation is,
In equation 1.5.3, a = f (S)
This states acceleration which is a function of distance.
Taking from the equation (1.4),
V dv = a dS
Or calculation for v dv = f (s) Ds
On integrating it, the calculated equation is,
Links of Previous Main Topic:-
- Introduction about distributed forces
- Area moments of inertia in rectangular and polar coordinates
- Mass moment of inertia introduction
- Work done by force
- Kinematics of particles
- Plane motion
Links of Next Mechanical Engineering Topics:-
- Graphical representation x y plane graph
- Distance travelled in the second in constant acceleration
- Acceleration due to gravity
- Position vector velocity and acceleration
- Plane kinematics of rigid bodies introduction
- Combined motion of translation and rotation
- Rectilinear motion in kinetics of particles