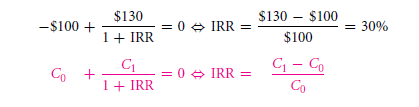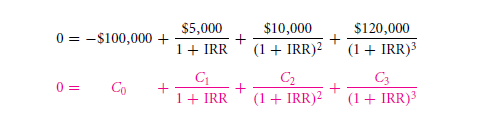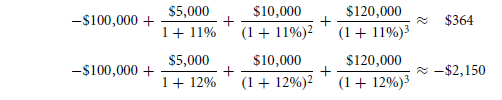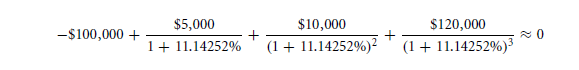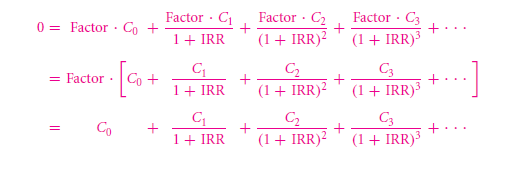Apart than the most common method of calculating the capital budgeting, this often may lead on a same place as per the renowned NPV rule. The most important method is very useful as it goes on through with a very different route and is often seen to provide as a good area of projection.
Let us get back to the project at hand, the one with certain cash flows. It translates as a rate of return which of a 20% value. The investment is of $100 and the pay return will be $120. The existing discount rate will be of a total 10%. This will be so as the rate of return of the project is that of 20% hence, it is and will be greater than the discount rate (10%). This is hence a very good one. The NPV project is thus positive with the example of $100 +$120/1.1 ~$9.10.
The only remaining existential problem remains to be as to how the value could be computed as the rate of return that too on a project or even a bond. Let us take an example as supposing an investment costs a total of $100000. This further pays a sum of $5000 in the gap of 1 year. The same value reaches up to $10000 in the duration of two years. And so on. Then what will the rate of return account to be of? Let us give it a thought shall we? The formula of rate of return works as only if there is an exact calculation of the total outflow and inflow. This is not definitely the ideal case here. The thing that you need is a total rate of return which can take up numerous flows both in and outflows which will further acknowledge into giving a total of rate of return which is near about that of the similar ones. This is called as the total internal rate of return. Hence, it is the measure that exists. It is an indicator of the rate to be intrinsic to the project. Thus it only depends on the cash flow course.
The true return rate which is created internally is in fact a very common site in context to the bonds and have acquired a name as to yield to maturity. There will be no notable difference among either one.
So, showing the internal; rate of return, it is essentially the simplest rate of return when there is only one cash inflow and also one out flow. Supposedly, if a project costs a total of $100 on today’s time, and further gives a sum of $130 in the coming year, then, the IRR is,
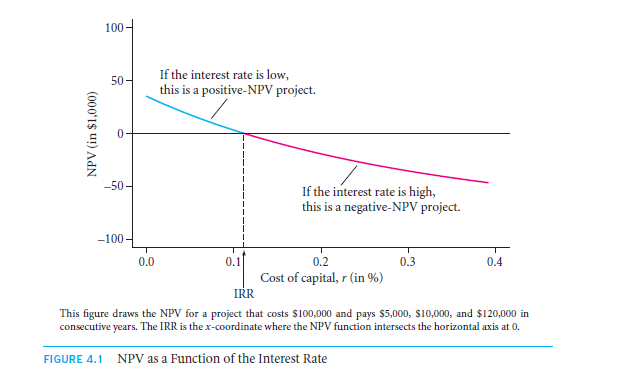
Considering an example that is simple and the rates of return will not be working, what will the correct number be which implies on the correct rate of return on a fellow projects that cost that of $100000 at the present market. This will further yield a value of the following consecutive values, $5000, $10000, $120000. What you might not be able to comprehend is that NPV of the particular project is like an ongoing interest rate value. If in case the discount rate is of a very lesser range than the definition will alter and will further be that of a peculiar and will be very low. The cash flows is not calculated simply and hence the four of the cash flows remain dormant. The total discount rate is that of low in this case. The total NPV will be positive. The way to solve and get the solution for this day is by,
The total discount rate is of a series of many set of equations of NPV to that of zero. In case that you wish to not determine the right value and to find the NPV function which crosses off to a zero axis. This is where you must learn to look for a solution of such complex equations that too by the method of trial and error. Always start along with two consecutive values like supposing 10% and 5%.
You must take the above given slide of 10% to reach to the level of zero. Hence, let us try out the other interest rates like 11% & 12%.
So, the main solution is definitely a closer version to that obtained by the percentage 11%. So here are a couple of other trial and error methods for you.
The rightful answer that you get to the project value is about of the percentage 11.4% IRR. What will be the thought of the internal rate of the return that is about to be avenged as the cash flow of the project.
There is absolutely no certain easy formula to measure out the IRR and if you will be dealing with a bigger number than the cash flows. The main automated trail and error method works to put the value of making a modern computer with many automated spreadsheets and even ones to solve all sorts of algebraic equations. On the table of 4.1, row number 1, this same thing is denoted and you can find out the total IRR that is required for the project and that is in the spreadsheet.
There is a negative on the cash flow pattern that is shown in the row number 2 and of the table 4.1 it shows that the rate is the same as IRR. This is of the received amount of inflow payment that is of $100000. This sum amount is followed by the values of payment like $5000, $10000, $120000 and will also display a percentage of 11.14252% IRR. What you can easily notice is that the case will look exactly like that of the IRR formula. The factors that are multiplied cancel out the impact over the solution number.
4.2a Projects With Multiple Or No IRRS
Many of the projects have a very big positive influence and also negative cash flows it can also have many internal return rates. On the aspect of taking an example, the project will be costing of a total of $100000, that will pay $205000, and this will have a cleanup of the cost value which is equivalent to that of $102000. The figure in the diagram 4.2 will project out the two different internal rates of returns in the taken aspect.
r = -15% &r =20%.
Confirming and computing this we will get that of:
Hence what is the supposedly internal rate of return? With the many cash flow returns, the percentages will be that of -15% and 20%. As an answer to both the anomalies, the entire rate of return will be stating out to be that which is valid for the definition. It is simply possible to make a cash flow out of the many dozens of the cash flows. So how come the computer made spreadsheets appear so flawless? We may never come across the reality and the explanation for it. What we know as of right now that it is mostly a random one where there is no sign of warning.
As for many projects, these may have many IRRs that other project levels do not have. As per the given example that lies in equivalent to that of the rates of returns, the project values will be yielding as to be $10 at the present day and $20 on the next day. These sorts of projects do not have any internal rate of returns. The NPV is never of a zero value. Let it be whatever the rate of return, there is simply no interest rates. As for the fact that the IRR of any given project does not appear to be from the cash flows. All of them have the similar aspects. This holds true for all the cash flows as they as having the same signs. However, what will the IRR be of a project that makes the same amount of cash like the cash flow spreadsheet be? in the figure of 4.2, it is depicted that the particular project will have no rates of returns that will turn the project to be a positive. Hence, it has no IRR. So, what is the computer depicted spreadsheets supposed to depict if there are no representation of the IRRs? They mostly display an error message in the maximum time period. They do so by alerting you of the in hand problem.
So, are you ready to really be sure of the project that anyone has to deal with? Is the only one uniquely distinguishing internal rate of return being a thing? As it likely makes out as the cash flow may be negative at any given time and the most common and close to investment pattern starts out as the project that you have in your hands. Projects that are of the many cash flows are supposed to be having various different positive as well as negative values. This can also make up to for the only IRR but hence it is not at all less popular. In any case, you can obviously rely on the unique IRRs as if the projects have so particular cash flow movement pattern. This is where the cash flow becomes a positive value that is immediately followed on by a negative one.
4.2B IRR As A Capital Budgeting Rule
IRR appears to be as important and useful in the calculations as it can be the perfect substitute for the true NPV just like that of the criterion for an investment.
Illustrating this, let us return to the project example that tends to cost the value of $100000 and gives of the value as yield of $5000, $10000, and $120000 with a total IRR value of 11.14%. The capital budgeting that is the IRR rules over the stated value that prevails on the long term economy. This is in fact the called and referred hurdled rate value. The finance percentage that comes about as a total of 11.20%.you must not take up this particular project to handle. If the percentage value comes around to be that of 11.10% only then are you supposed to take a go o step towards this project. A NPV offering as the same one on the recommendation? So try it off.
You must get the equal and or equivalent recommendation record.
In the case where supposedly, the cash flow comes out to be the exact opposite value of the one, you will receive $100000 as a hand over value. This will later pay off the sum of $5000 $100000 and also $120000. Therefore, in such a case, this will not be the condition where the investment project is marvelous. All that you need is a good investment project that too with a good ongoing interest rate that will be stated on the higher scale of 11.14%. All that you need to be cautious is about the IRR to be below or on a rate that is above the hurdle rate that is mentioned earlier. I would advise to stay clear of the mistakes that most people make while working on the total formula of NPV investment.
As to why use the IRR, when you can just use the NPV lies on the advantage that this offers. The former one i.e. the IRR is a convenient calculation method that gives the rightly calculated rates. These rates are very convenient to effectively trace and calculate. The IRR is a very efficient method, though a little broad, it calculates the righteous interest rate or the appropriate cost of capital in a project. The IRR gives very useful information and also helps in the judging of the area of role of a managing head. This makes it awfully easy to handle a close firm grip on the delivering promise on the IRR that is of a total 20%. This will be a much more satisfying thing than having to argue as to what the cost of capital must be for a definite project.
4.2c Problems With IRR As A Capital Budgeting Rule
In case you start using the IRR in a correct fashion, the rightful circumstances lead on to form that of the NPV rule. You can further do this deal much better than the way that you are doing it presently. As for the ways, it remains to be a safe method to use the NPV formula rule instead of the IRR method rule. What does this IRR in the field of capital budgeting make the working look like? Well, one thing is for sure that the uniqueness of the IRR is a very sophisticated methodology. In this course, it becomes very clear that the deal that you make is the deal that you get. If the project on hand gives you a good layout format, then the chances are that you will want to take it. In the world of financing, you are bound to make the IRR that is listed down to make the capital cut off its costs. So, I would advice you to check on the IPP formula to make a calculation of the right NPV.
However, if due to some unfortunate circumstances, if the IRR is not a unique value or not.The projects that are made up of various criterions without being a painful anomaly. Let us concentrate with an example,
The existing cost of capital or the interest rate being a 9% is a project value that is of 6% 8% and also 10%. So, must you go opt for the project? Or must you simply avoid it?
The answer is not at all a very easy one. To make up any investment decision that is if you are to take back the decision part, then would you? The total part that you get from an NPV graph is of a particular form and not the other. Getting the hold of the number is however, very easy and awfully possible. In a situation if you have a project, then I would suggest you to avoid taking in the investment decision which will make the drawing of the summation as an easy that is on a remaining cost of capital that is 9%. The total decision that you make for the NPV graph is laid to rest when the calculation is done for the IRR percentage.
Measuring that you do for the multiple solutions is not something that you must let your self bother about. As for the NPV elimination, the 0 axis will give off an easy set of circumstances which will be that of working with a total of the IRR that only begs on for more attention. In the case where there is no IRR in a particular project, then, you will ultimately have to turn your attention to NPV discount rate. The 0 axis will turn out to be a massive old school thing. both of these things will accompany up into getting the project out to be lost in the differences. the main problems sum up to as the ones of IRR being used.
The troubles that you most certainly need to keep in your mind are that there are further problems mainly 2 which are equally involved in the demeanor:
- Project comparisons and scale: the main assertive value that is placed for the IRR can be very misleading and as to the importance of the projects in hand these rates are very different to the ones that are accosted. In case that one person had to choose the ones that the IRR would be of 100% on a project of 10% . So, getting to learn about it, if the initial project is ought to be that with an opportunity to invest a maximum of $5, and then the returning rate would be that of $1000. The discount rate that strikes the mind is that of a total 5% on a yearly basis.
This will be so for only any particular project center, with one project to be listed as B and the one with lower IRR rate to be A.
- Cost of capital comparison: on the upcoming chapter, the long term investing rates of interests will be explained which remain to be at a much higher value. the short term interest rates will remain and take the position to be on the bottom rather than that of the long term interest rate. A one year total treasury bond that you get is hence offered on to people by the rate of return of 6%. In the assumption of a risk-free project, the IRR must be of a value of 4% too?
Both these problems lie as a project of isolation. In the real world, however, the project analysis is mostly overlooked.
Links of Previous Main Topic:-
- Introduction of corporate finance
- The time value of money and net present value
- Stock and bond valuation annuities and perpetuities
- A first encounter with capital budgeting rules
- Net present value chapter 4
Links of Next Financial Accounting Topics:-