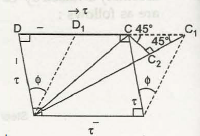
To understand the relationship between E and G, take square block ABCD
Shear strain = ϕ
Strain of AC = AC1 – AC / AC = C1 C2 / AC
= CC1 cos 45° / √2 = CC1 / 2 AB
1 /2 (CC1 / AB) = 1/2 (CC1 / BC) = 1/2 ϕ
= 1/2 x t / G
Again, AC has the tensile strain and it takes place due to the stress
σ = σ / E
= t / E
On the diagonal AC the tensile stress takes place because of the compressive stress on BD
= µ . t /E
Combined effect of the two different stresses on the given
Diagonal AC = t / E + µ t /E = t /E (1+µ)
By equating both the equation, we have
t = 2G = t / E (1+µ)
G = E / 2 (1 +µ)
where ,
µ = Poisson’s ratio
G = modulus of rigidity
E = modulus of elasticity.
Links of Previous Main Topic:-
- Linear momentum
- Force mass acceleration
- Simple stress introduction
- Normal strain
- Statically indeterminate system
- Thermal stresses
Links of Next Mechanical Engineering Topics:-